Cho dãy số (un) : \(0;\frac{1}{2};\frac{2}{3};\frac{3}{4};\frac{4}{5};....\) Số hạng tổng quát của dãy số (un) là :
A. \(u_n=\frac{n-1}{n}\)
B. \(u_n=\frac{n}{n+1}\)
C. \(u_n=\frac{n^2-n}{n+1}\)
D. \(u_n=\frac{n+1}{n+2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
24 tháng 4 2017
Lấy số dương ε bé tùy ý bất kì:
⇒ có một số n0 thỏa mãn: |vn| < ε kể từ n = n0.
⇒ |un – 2| < vn < |vn| < ε kể từ n = n0 trở đi
⇒ lim (un – 2) = 0
⇒ lim un = 2.
CM
22 tháng 7 2018
a) Khoảng cách từ un tới 0 trở nên rất nhỏ (gần bằng 0) khi n trở nên rất lớn
b) Bắt đầu từ số hạng u100 của dãy số thì khoảng cách từ un đến 0 nhỏ hơn 0,01
Bắt đầu từ số hạng u1000 của dãy số thì khoảng cách từ un đến 0 nhỏ hơn 0,001
CM
2 tháng 3 2017
l i m v n = 0 ⇒ | v n | có thể nhỏ hơn một số dương bé tuỳ ý, kể từ một số hạng nào đó trở đi (1)
Vì | u n | ≤ v n v à v n ≤ | v n | với mọi n, nên | u n | ≤ | v n | với mọi n. (2)
Từ (1) và (2) suy ra | u n | cũng có thể nhỏ hơn một số dương bé tuỳ ý, kể từ một số hạng nào đó trở đi, nghĩa là l i m u n = 0
CM
7 tháng 12 2017
Chọn B.
Ta có: u1 = 1; u2 = 3/2; u3 = 17/6; u4 = 227/34.
Ta chứng minh un > 0 bằng quy nạp.
Giả sử un > 0, khi đó: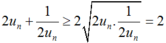 
Nên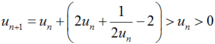 
.
và 
.
CM
2 tháng 7 2019
Vì ( u n ) có giới hạn là 0 nên | u n | có thể nhỏ hơn một số dương bé tuỳ ý, kể từ một số hạng nào đó trở đi.
Mặt khác, | v n | = | | u n | | = | u n | . Do đó, | v n | cũng có thể nhỏ hơn một số dương bé tuỳ ý, kể từ một số hạng nào đó trở đi. Vậy ( v n ) có giới hạn là 0.
B