Trong không gian với hệ tọa độ Oxyz, cho A(1;0;1) và B(-1;-3) và mặt phẳng \(\left(\alpha\right):x+2y+3z+3=0\), lập phương trình đường thẳng\(\left(\beta\right)\) đi qua 2 điểm A, B và vuông góc với mặt phẳng \(\left(\alpha\right)\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
2 tháng 10 2017
Đáp án A
Ta có xA' = 2xO-xA = 3; yA' = 2yO-yA = -2; zA' = 2zO-zA=1. Vậy A'(3;-2;1).
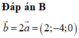

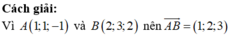

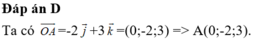
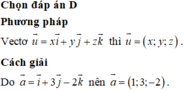
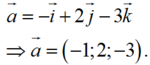
\(\overrightarrow{n}=\left[\overrightarrow{AB};\overrightarrow{n_{\alpha}}\right]=\left(1;-2;1\right)\) là một vectơ pháp tuyến của \(\left(\beta\right)\)
Mặt phẳng \(\beta\) đi qua A có vectơ pháp tuyến \(\overrightarrow{n}=\left(1;-2;1\right)\) có phương trình \(x-2y+z-2=0\)
Cho x, y là các số thỏa mãn \(x^2+y^2+xy=3\Leftrightarrow\left(x+y\right)^2-3=xy\)
Vì \(xy\le\frac{\left(x+y\right)^2}{4}\Leftrightarrow\left(x+y\right)^2-3\le\frac{\left(x+y\right)^2}{4}\)
\(\Leftrightarrow\left(x-y\right)^2\le4\)