với mỗi số x thuộc R, ta gọi f(x) là GTNN trong các số 4x+1;x+2;-2x+6.
a) vẽ đồ thị y=f(x);
b) Tìm Max f(x)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y=f\left(x\right)=4x^2-9\)
a, \(f\left(-2\right)=4.\left(-2\right)^2-9\)
\(=16-9\)
\(=7\)
\(f\left(-\dfrac{1}{2}\right)=4.\left(-\dfrac{1}{2}\right)^2-9\)
\(=4.\dfrac{1}{4}-9\)
\(=1-9\)
\(=-8\)
b, \(f\left(x\right)=-1\Rightarrow4x^2-9=-1\)
\(\Leftrightarrow4x^2=8\)
\(\Leftrightarrow x^2=2\)
\(\Leftrightarrow\)\(x=\pm\sqrt[]{2}\)
c, Ta có \(f\left(x\right)=4x^2-9\)
\(f\left(-x\right)=4\left(x\right)^2-9\)
\(=4x^2-9\) \(=f\left(x\right)\)
Vậy \(f\left(x\right)=f\left(-x\right)\)
-Chúc bạn học tốt-

\(\Leftrightarrow\left(x-y+m\right)^2+y^2+2\left(m+1\right)y-m^2+25\ge0\); \(\forall x;y\)
\(\Leftrightarrow y^2+2\left(m+1\right)y-m^2+25\ge0\) ;\(\forall y\)
\(\Leftrightarrow\Delta'=\left(m+1\right)^2-\left(-m^2+25\right)\le0\)
\(\Leftrightarrow m^2+m-12\le0\Rightarrow-4\le m\le3\)

Chọn đáp án C
*Trường hợp 1:
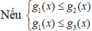
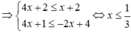
![]()
Do hàm số g 1 x = 4 x + 1 đồng biến trên ( - ∞ ; 1 3 ]
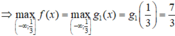

\(f\left(x\right)+3f\left(\frac{1}{x}\right)=x^2\)
Thế \(x=2\)ta được:
\(f\left(2\right)+3f\left(\frac{1}{2}\right)=4\)
Thế \(x=\frac{1}{2}\)ta được:
\(f\left(\frac{1}{2}\right)+3f\left(2\right)=\frac{1}{4}\)
Ta có hệ phương trình:
\(\hept{\begin{cases}f\left(2\right)+3f\left(\frac{1}{2}\right)=4\\3f\left(2\right)+f\left(\frac{1}{2}\right)=\frac{1}{4}\end{cases}}\Leftrightarrow\hept{\begin{cases}f\left(2\right)=-\frac{13}{32}\\f\left(\frac{1}{2}\right)=\frac{47}{32}\end{cases}}\)

\(x=2\Rightarrow f\left(2\right)+3.f\left(\frac{1}{2}\right)=4\)
\(x=\frac{1}{2}\Rightarrow f\left(\frac{1}{2}\right)+3.f\left(2\right)=\frac{1}{4}\)
\(\Rightarrow f\left(2\right)=\frac{47}{32}\)
kết quả nhanh nhất
= 47/32
h mk nha bn hiền
chúc bn học giỏi