Cho hàm số y=\(\dfrac{1}{4}\)x2 . Xác định a,b để đường thẳng [d] ; y=ax+b cắt trục tung tại điểm có tung độ =-2 và cắt đồ thị [P] nói trên tại điểm có hoành độ =2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
a) Để hàm số y=(k-2)x+k+3 là hàm số bậc nhất thì \(k\ne2\)
b) Để hàm số y=(k-2)x+k+3 đồng biến trên R thì k-2>0
hay k>2
Bài 2:
Thay \(x=-\dfrac{1}{2}\) và \(y=\dfrac{2}{3}\) vào (D), ta được:
\(\left(2m-3\right)\cdot\dfrac{-1}{2}-\dfrac{1}{2}=\dfrac{2}{3}\)
\(\Leftrightarrow\left(2m-3\right)\cdot\dfrac{-1}{2}=\dfrac{2}{3}+\dfrac{1}{2}=\dfrac{7}{6}\)
\(\Leftrightarrow2m-3=\dfrac{7}{6}:\dfrac{-1}{2}=\dfrac{-7}{6}\cdot\dfrac{2}{1}=-\dfrac{14}{6}=-\dfrac{7}{3}\)
\(\Leftrightarrow2m=\dfrac{-7}{3}+3=\dfrac{-7}{3}+\dfrac{9}{3}=\dfrac{2}{3}\)
hay \(m=\dfrac{1}{3}\)

a: Thay x=7 và y=2 vào (d), ta được:
7(m+1)+m-1=2
=>7m+7+m-1=2
=>8m+6=2
=>8m=-4
=>\(m=-\dfrac{1}{2}\)
b: Thay x=2 vào y=3x-4, ta được:
\(y=3\cdot2-4=2\)
Thay x=2 và y=2 vào (d), ta được:
2(m+1)+m-1=2
=>2m+2+m-1=2
=>3m+1=2
=>3m=1
=>\(m=\dfrac{1}{3}\)
c: Tọa độ giao điểm của hai đường d1 và d2 là:
\(\left\{{}\begin{matrix}2x-1=x-8\\y=2x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-x=-8+1\\y=2x-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-7\\y=2\left(-7\right)-1=-15\end{matrix}\right.\)
Thay x=-7 và y=-15 vào d, ta được:
\(-7\left(m+1\right)+m-1=-15\)
=>-7m-7+m-1+15=0
=>-6m+7=0
=>-6m=-7
=>\(m=\dfrac{7}{6}\)

c: Để (d) vuông góc với (Δ) thì \(\left(6m+1\right)\cdot6=-1\)
\(\Leftrightarrow6m+1=-\dfrac{1}{6}\)
hay \(m=-\dfrac{7}{36}\)

a) Thay x=1 và y=2 vào (P), ta được:
\(a\cdot1^2=2\)
hay a=2

(P): \(y=2x^2\)
Phương trình hoành độ giao điểm (P) và (d):
\(2x^2=mx-m^2-\dfrac{3}{2}m-\dfrac{3}{4}\)
\(\Leftrightarrow2x^2-mx+m^2+\dfrac{3}{2}m+\dfrac{3}{4}=0\) (1)
\(\Delta=m^2-8\left(m^2+\dfrac{3}{2}m+\dfrac{3}{4}\right)=-7m^2-12m-6=-7\left(m+\dfrac{6}{7}\right)^2-\dfrac{6}{7}< 0\) ; \(\forall m\)
\(\Rightarrow\) (1) vô nghiệm với mọi m hau (d) và (P) ko cắt nhau với mọi m

Với m = 0 ta có: y = x 3 – 4 x 2 – 4x.
Đường thẳng y = kx sẽ cắt (C) tại ba điểm phân biệt nếu phương trình sau có ba nghiệm phân biệt: x 3 – 4 x 2 – 4x = kx.
Hay phương trình x 2 – 4x – (4 + k) = 0 có hai nghiệm phân biệt khác 0, tức là:
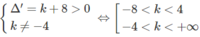

vì đường thẳng cắt điểm có tung độ = -2 nên x=0,y=-2 thay x=0,y=-2 vào (d) ta được: b=-2 vì đường thẳng cắt đồ thị (P) có hoành độ =2 nên x=2,y=0 thay x=2,y=0 vào (d) ta được ; 2a + (-2) =0 hay a=1 vậy a=1 , b=-2 là giá trị cần tìm