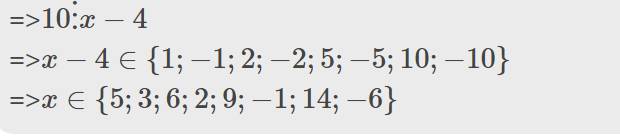Cho biểu thức : M = 1-2+3-4+5-6+...+35-36 . Tìm các số nguyên x ; y sao cho 5x - 2xy = M
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Các bạn giúp mình giải với nhé! Đúng thì mình k đúng nhé. Cảm ơn các bạn nhiều lắm. Yêu cả nhà.
\(1.\left(x-5\right)^{23}.\left(y+2\right)^7=0\)
\(\Rightarrow\hept{\begin{cases}\left(x-5\right)^{23}=0\\\left(y+2\right)^7=0\end{cases}\Rightarrow\hept{\begin{cases}\left(x-5\right)^{23}=0^{23}\\\left(y+2\right)^7=0^7\end{cases}}}\)\(\Rightarrow\hept{\begin{cases}x-5=0\\y+2=0\end{cases}\Rightarrow\hept{\begin{cases}x=0+5\\y=0-2\end{cases}}}\)\(\Rightarrow\hept{\begin{cases}x=5\\y=-2\end{cases}}\)
Vậy \(\left(x;y\right)=\left(5;-2\right)\)

1: \(D=\dfrac{1}{x+4}+\dfrac{x}{x-4}+\dfrac{24-x^2}{x^2-16}\)
\(=\dfrac{1}{x+4}+\dfrac{x}{x-4}+\dfrac{24-x^2}{\left(x+4\right)\left(x-4\right)}\)
\(=\dfrac{x-4+x\left(x+4\right)+24-x^2}{\left(x+4\right)\left(x-4\right)}\)
\(=\dfrac{-x^2+x+20+x^2+4x}{\left(x+4\right)\left(x-4\right)}=\dfrac{5x+20}{\left(x+4\right)\left(x-4\right)}\)
\(=\dfrac{5\left(x+4\right)}{\left(x+4\right)\left(x-4\right)}=\dfrac{5}{x-4}\)
2: Khi x=10 thì \(D=\dfrac{5}{10-4}=\dfrac{5}{6}\)
3: \(M=\left(x-2\right)\cdot D=\dfrac{5\left(x-2\right)}{x-4}\)
Để M là số nguyên thì \(5\cdot\left(x-2\right)⋮x-4\)
=>\(5\left(x-4+2\right)⋮x-4\)
=>\(5\left(x-4\right)+10⋮x-4\)
=>\(10⋮x-4\)
=>\(x-4\in\left\{1;-1;2;-2;5;-5;10;-10\right\}\)
=>\(x\in\left\{5;3;6;2;9;-1;14;-6\right\}\)

Bài 5:
\(C=\frac{2\sqrt{x}-3}{\sqrt{x}-2}=\frac{2(\sqrt{x}-2)+1}{\sqrt{x}-2}=2+\frac{1}{\sqrt{x}-2}\)
Để $C$ nguyên nhỏ nhất thì $\frac{1}{\sqrt{x}-2}$ là số nguyên nhỏ nhất.
$\Rightarrow \sqrt{x}-2$ là ước nguyên âm lớn nhất
$\Rightarrow \sqrt{x}-2=-1$
$\Leftrightarrow x=1$ (thỏa mãn đkxđ)
Bài 6:
$D(\sqrt{x}+1)=x-3$
$D^2(x+2\sqrt{x}+1)=(x-3)^2$
$2D^2\sqrt{x}=(x-3)^2-D^2(x+1)$ nguyên
Với $x$ nguyên ta suy ra $\Rightarrow D=0$ hoặc $\sqrt{x}$ nguyên
Với $D=0\Leftrightarrow x=3$ (tm)
Với $\sqrt{x}$ nguyên:
$D=\frac{(x-1)-2}{\sqrt{x}+1}=\sqrt{x}-1-\frac{2}{\sqrt{x}+1}$
$D$ nguyên khi $\sqrt{x}+1$ là ước của $2$
$\Rightarrow \sqrt{x}+1\in\left\{1;2\right\}$
$\Leftrightarrow x=0; 1$
Vì $x\neq 1$ nên $x=0$.
Vậy $x=0; 3$