Cho ba hàm số:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a; f(0)=0
f(-1/3)=-1
b: y=-6 thì 3x=-6
hay x=-2
y=12 thì 3x=12
hay x=4

a: Thay x=-1 và y=1 vào (d), ta được:
-(2m+1)=1
=>2m+1=-1
=>2m=-2
=>m=-1
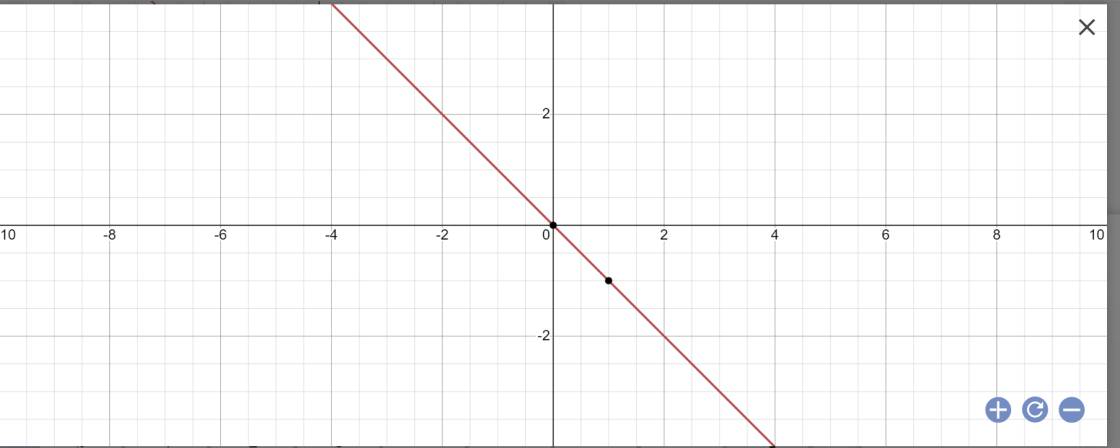
b: y=(-2+1)x=-x

f(-1)=b-a=10
f(1)=b+a=6
=>b=(10+6):2=8=> a=6-8=-2
Vậy a=-2,b=8

Tham khảo: tìm GTLN - GTNN của hàm số : y=sinx cosx sinxcosx - Hoc24
Đặt sinx+cosx=t⇒−√2≤t≤√2sinx+cosx=t⇒−2≤t≤2
t2=sin2x+cos2x+2sinx.cosx=1+2sinx.cosx⇒sinx.cosx=t2−12t2=sin2x+cos2x+2sinx.cosx=1+2sinx.cosx⇒sinx.cosx=t2−12
⇒y=t+t2−12=12
Đặt \(sinx+cosx=\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=t\Rightarrow t\in\left[-\sqrt{2};\sqrt{2}\right]\)
\(t^2=1+2sinx.cosx\Rightarrow sinx.cosx=\dfrac{t^2-1}{2}\)
\(\Rightarrow y=t+\dfrac{t^2-1}{2}=\dfrac{1}{2}t^2+t-\dfrac{1}{2}\)
Xét hàm \(y=f\left(t\right)=\dfrac{1}{2}t^2+t-\dfrac{1}{2}\) trên \(\left[-\sqrt{2};\sqrt{2}\right]\)
\(-\dfrac{b}{2a}=-1\in\left[-\sqrt{2};\sqrt{2}\right]\)
\(f\left(-\sqrt{2}\right)=\dfrac{1-2\sqrt{2}}{2}\) ; \(f\left(-1\right)=-1\) ; \(f\left(\sqrt{2}\right)=\dfrac{1+2\sqrt{2}}{2}\)
\(\Rightarrow y_{min}=-1\) ; \(y_{max}=\dfrac{1+2\sqrt{2}}{2}\)

bn có thể vào đây xem nhé https://lazi.vn/edu/exercise/ve-do-thi-cua-ham-so-y-2x

Lời giải:
TXĐ: $D=\mathbb{R}$
Lấy $x_1\neq x_2\in D$. Xét:
$A=\frac{f(x_1)-f(x_2)}{x_1-x_2}$
\(=\frac{\frac{x_1^3}{x_1^2+1}-\frac{x_2^3}{x_2^2+1}}{x_1-x_2}=\frac{x_1^2x_2^2+x_1^2+x_1x_2+x_2^2}{(x_1^2+1)(x_2^2+1)}>0\) với mọi $x_1,x_2\in\mathbb{R}; x_1\neq x_2$
Do đó hàm số luôn đồng biến trên $\mathbb{R}$


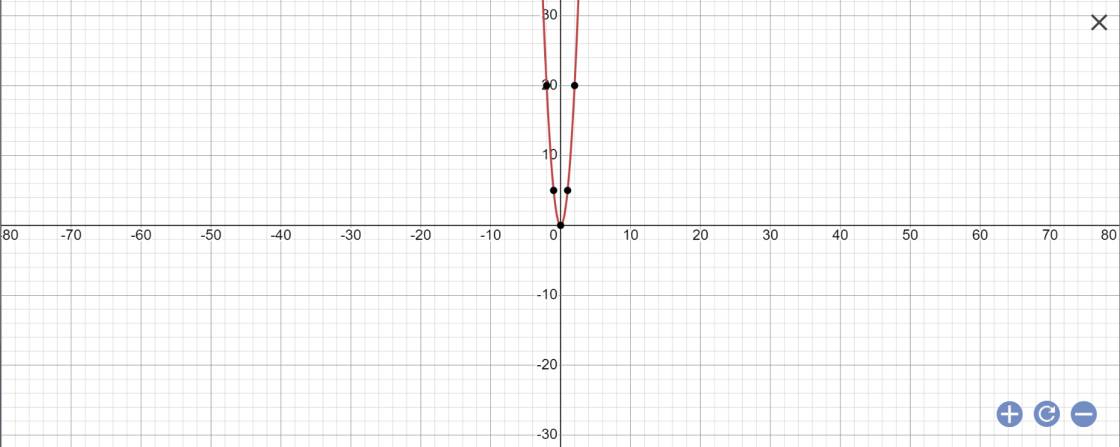
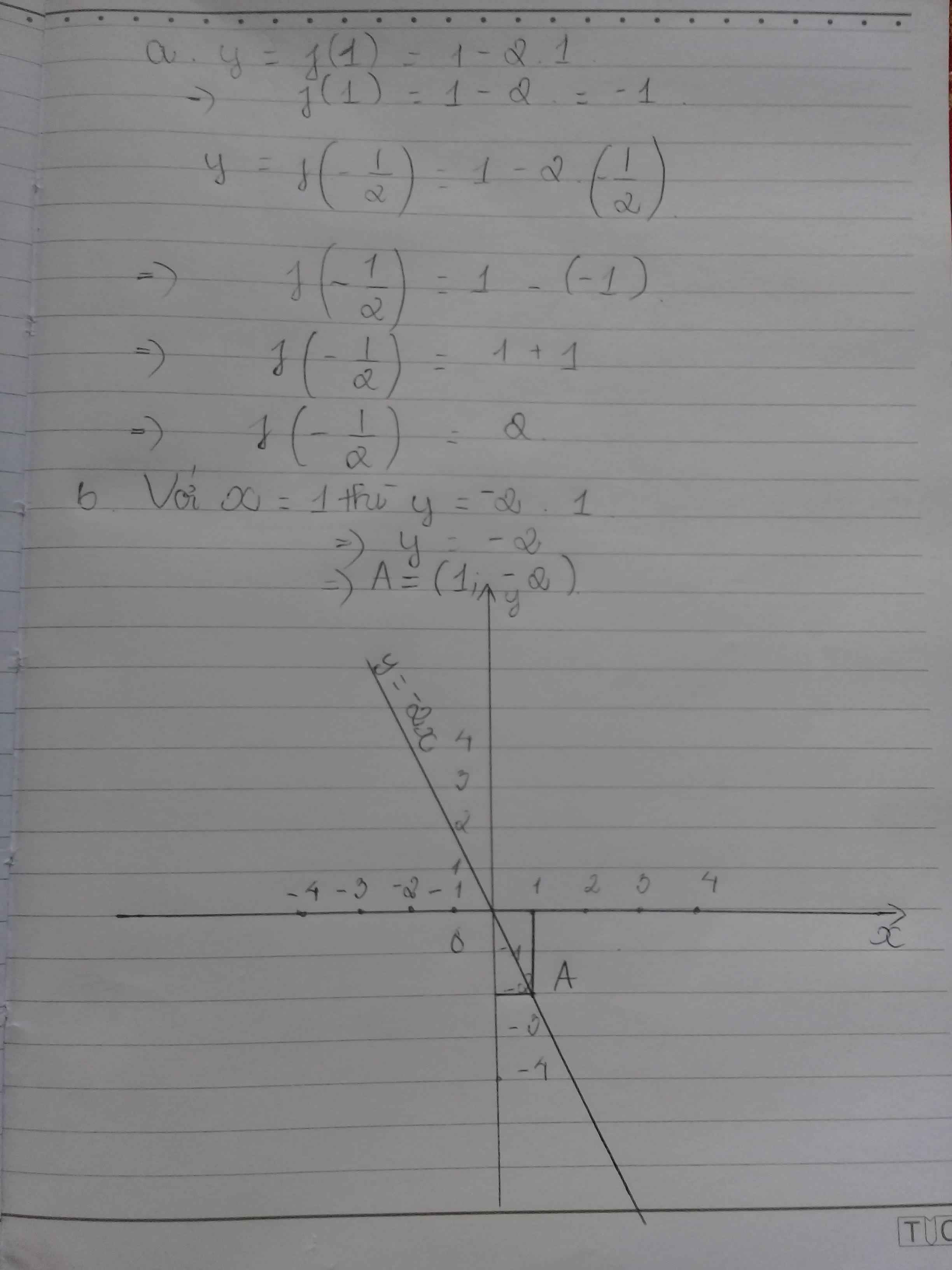
a) Vẽ đồ thị
b) Gọi yA, yB, yC lần lượt là tung độ các điểm A, B, C có cùng hoành độ x = -1,5. Ta có:
yA = . (-1,5)2 =
. (-1,5)2 =  . 2,25 = 1,125
. 2,25 = 1,125
yB = (-1,5)2 = 2,25
yC = 2 (-1,5)2 = 2 . 2,25 = 4,5
c) Gọi yA, yB, yC’ lần lượt là tung độ các điểm A', B', C' có cùng hoành độ x = 1,5. Ta có:
yA, = . 1,52 =
. 1,52 =  . 2,25 = 1,125
. 2,25 = 1,125
yB, = 1,52 = 2,25
yC’ = 2 . 1,52 = 2 . 2,25 = 4,5
Kiểm tra tính đối xứng: A và A', B và B', C và C' đối xứng với nhau qua trục tung Oy.
d) Với mỗi hàm số đã cho ta đều có hệ số a > 0 nên O là điểm thấp nhất của đồ thị. Khi đó ta có x = 0.
Vậy x = 0 thì hàm số có giả trị nhỏ nhất.