Cho ∆ABC (A= 900 ); BD là phân giác của góc B (D∈AC); vẽ DE⊥BC. Gọi F là giao điểm của AB và DE
a)Chứng minh Δ ABD = ΔEBD và BD là đường trung trực của AE.
b) Chứng minh Δ DCF cân
c) Khi ∆ABC có B= 600 ; C= 300 và BC = 12 cm . Tính độ dài DC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
A
💋Amanda💋
2 tháng 3 2020
https://i.imgur.com/DEXxgq4.jpg
Đúng(0)
Những câu hỏi liên quan
CM
21 tháng 8 2019
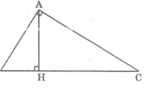
Xét hai tam giác vuông HBA và HAC, ta có:
∠ (AHB) = ∠ (AHC) = 90 0
∠ B = ∠ (HAC) (hai góc cùng phụ C )
Suy ra: △ HBA đồng dạng △ HAC (g.g)
Suy ra: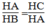 
Vậy A H 2 = B H . C H
CM
20 tháng 12 2019
Xét ∆ ABC vuông tại A ta có: A B = B C . sin α = a . sin α A C = B C . cos α = a . c o s α
Đáp án cần chọn là: A
CM
15 tháng 1 2019
Ta có: ΔABC cân tại A
⇒ AE là đường cao đồng thời là đường phân giác ∠BAC.
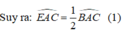
+) Tam giác ABC cân tại A nên AB = AC.
Lại có: AD = AB( giả thiết)
Suy ra: AD = AC
Do đó: ΔADC cân tại A
+) Trong tam giác ADC có: AF là đường caon nên đồng thời là đường phân giác ∠CAD.
CM
12 tháng 3 2017
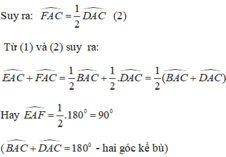
S A B C = . AB. AC ≤ 1 2 . A B 2 + A C 2 2 = 1 4 . A B 2 + A C 2
Áp dụng định lý Py-ta-go cho ABC vuông tại A ta có:
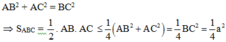
Dấu “=” xảy ra AC = AB => ∆ ABC vuông cân
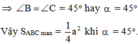
Đáp án cần chọn là: D