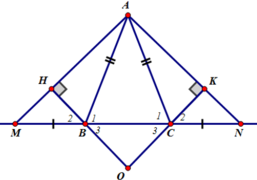
cho tam giác ABC cân tại A trên tia đối BC lấy M ; trên tia đối CB lấy N sao cho MB=BC=CN
BH vuông góc AM ( H thuộc AM)
CK vuông góc AN ( K thuộc AN)
HB cắt KC tại O
chứng minh MO=ON=AO
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì tam giác ABC cân tại A
\(\Rightarrow\left\{{}\begin{matrix}AB=AC\\\text{^}B_1=\text{^}C_1\end{matrix}\right.\)
Xét tam giác ABM và tam giác ACN có:
\(AB=AC\)(gt)
\(\text{^}B_2=\text{^}C_2\left(Vì\text{^}B_1=\text{^}C_1\right)\)
\(BM=CM\left(gt\right)\)
⇒ Tam giác ABM= tam giác ACN (c.g.c)
⇒ \(AM=AN\) (t/ứ)
⇒ Tam giác AMN cân tại A (đpcm)

a: Ta có: ΔABC cân tại A
nên AB=AC
b: Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
c: Ta có: ΔABM=ΔACN
nên AM=AN
hay ΔAMN cân tại A


ΔABC cân tại A suy ra 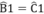
Ta lại có :
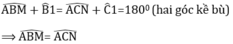
- ΔABM và ΔACN có
AB = AC (Do ΔABC cân tại A).
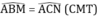
BM = CN(gt)
⇒ ΔABM = ΔACN (c.g.c)
⇒ AM = AN (hai cạnh tương ứng) ⇒ ΔAMN cân tại A.

Xét ΔBAM và ΔCAN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
DO dó: ΔBAM=ΔCAN
Suy ra: AM=AN
hay ΔAMN cân tại A

Từ đỉnh A kẻ đường cao AH (H thuộc BC) (1)
Ta có : tam giác ABC cân tại A (gt) (2)
Từ(1) và(2)=> HB=HC(=1/2 BC) (3)
Lại có: BM=CN (gt) (4)
M nằm trên tia đối của tia BC, N nằm trên tia đối của tia CB => M,B,C.N thẳng hàng (5)
Từ (3)và (4)=>HB+BM=HC+CN (6)
Từ (5) và (6)=>AH vừa là đường cao, vừa là đường trung tuyến trong tam giác AMN
=> Tam giác AMN cân tại A (đpcm)

a: Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
=>ΔABD=ΔACE
=>AD=AE
=>ΔADE cân tại A
b: ΔABC cân tại A có AM là trung tuyến
nên AM vuông góc BC
ΔADE cân tại A có AM là đường cao
nên AM là phân giác của góc DAE
a
Theo đề có \(\widehat{ABC}=\widehat{ACB}\) (tam giác ABC cân tại A)
Lại có: \(\widehat{ABD}+\widehat{ABC}=\widehat{ACE}+\widehat{ACB}\left(=180^o\right)\)
\(\Rightarrow\widehat{ABD}=\widehat{ACE}\)
Xét tam giác ABD và tam giác ACE có:
`AB=AC`
\(\widehat{ABD}=\widehat{ACE}\left(cmt\right)\)
`DB=CE`
=> ΔABD = ΔACE
=> `AD=AE` (2 cạnh tương ứng)
=> Tam giác ADE cân tại A
b
Ta có:
`BM=CM`
`DB=CE`
\(\Rightarrow\)`DM=EM`
\(\Rightarrow\)AM là đường trung tuyến của ΔADE
\(\Rightarrow\)AM là tia phân giác của \(\widehat{DAE}\)
G/s: MO = OA
Dễ dàng chứng minh AO là đường trung trực MN và BC
=> Tam giác AOM cân tại O và B là giao điểm hai đường cao => B là trực tâm
=> AB vuông OM
Dễ dàng chứng minh AB = BM mà BM = BC
=> AB = BC => tam giác ABC đều => Vô lí với giả thiết
Em kiểm tra lại đề nhé!
Nguyễn Linh Chi
a chết sr cô ạ con thiếu đề : \(\widehat{BAC}\)