Cho góc xOy, lấy điểm A; B thuộc tia Ox, lấy điểm CD thuộc tia Oy; sao cho OA = OC; OB = OD. Gọi E là giao điểm của AD và BC. Chứng minh rằng:
a) AD = BC
b) Tam giác EAD = tam giác ECD
c) OE là phân giác góc xOy
Giúp mih vs. Mih c.ơn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 1 2024
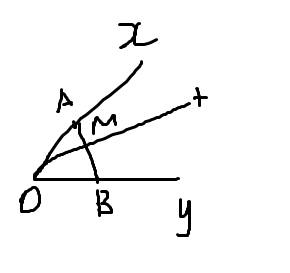
a. OA=OB
⇒ΔOAB cân tại O
mà OM là phân giác góc AOB
nên OM là đường trung tuyến ΔAOB
⇒M là trung điểm AB ⇒MA=MB
b. Xét ΔOAM và ΔOBM, có
OA=OB
OM chung
MA=MB
⇒ΔOAM = ΔOBM
nên OMA=OMB (đpcm)
6 tháng 12 2023
Ta có: M là trung điểm của AB
=>MA=MB
Xét ΔOAM và ΔOBM có
OA=OB
AM=BM
OM chung
Do đó: ΔOAM=ΔOBM
=>\(\widehat{AOM}=\widehat{BOM}\)
=>\(\widehat{xOM}=\widehat{yOM}\)
mà tia OM nằm giữa hai tia Ox,Oy
nên OM là phân giác của \(\widehat{xOy}\)
23 tháng 6 2019
y x O M A B 1 2
Xét tam giác OMA và tam giác OMB ,có :
OM chung
góc O1 = góc O2 ( gt )
OA = OB ( gt )
=> tam giác OMA = tam giác OMB ( c-g-c )
=> MA = MB ( hai cạnh tương ứng )
=> tam giác AMB cân tại A
Vậy tam giác AMB cân
7 tháng 10 2021
Bài 4:
a: Xét ΔABC vuông tại A và ΔABD vuông tại A có
BA chung
AC=AD
Do đó: ΔABC=ΔABD
b: Xét ΔMAC vuông tại A và ΔMAD vuông tại A có
MA chung
AC=AD
Do đó: ΔMAC=ΔMAD
Xét ΔMBD và ΔMBC có
MB chung
BD=BC
MD=MC
Do đó: ΔMBD=ΔMBC
Ta có hình vẽ :
O A B C D E x y
a/ Xét tam giác OAD và tam giác OBC có:
OA = OC (GT)
OˆO^: góc chung
OB = OD (GT)
=> tam giác OAD = tam giác OBC (c.g.c)
=> AD = BC (2 cạnh tương ứng)
b/ Ta có: BˆB^=DˆD^ (vì tam giác OAD = tam giác OBC) (1)
Ta có: {OA=OCOB=OD{OA=OCOB=OD⇒AB=CD⇒AB=CD (2)
Ta có: OADˆOAD^=OCBˆOCB^ (vì tam giác OAD = tam giác OBC) (*)
+)Ta có: OADˆOAD^+DABˆDAB^=1800 (**)
+) Ta có: OCBˆOCB^+BCDˆBCD^=1800 (***)
Từ (*),(**),(***) => DABˆDAB^=BCDˆBCD^ (3)
Từ (1),(2),(3) => tam giác EAB = tam giác ECD
c/ Xét tam giác OAE và tam giác OCE có:
OA = OC (GT)
AE = EC (vì tam giác EAB = tam giác ECD)
OE: cạnh chung
=> tam giác OAE = tam giác OCE (c.c.c)
=> AOEˆAOE^=COEˆCOE^ (2 góc tương ứng)
=> OE là phân giác xOyˆxOy^ (đpcm)