n điểm ( n € N ; n = hoặc > 3)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
24 tháng 2 2018
Vẽ bốn điểm M, N, P, Q thẳng hàng theo mỗi cách diễn đạt sau:
a) Điểm N nằm giữa hai điểm M và P. Điểm Q nằm giữa hai điểm N và P.
b) Điểm Q và điểm M nằm khác phía với điểm N. Điểm P nằm giữa hai điểm N và Q.
c) Điểm M và điểm P nằm cùng phía với điểm N. Điểm P không nằm giữa hai điểm M và N. Điểm Q nằm giữa hai điểm M và N.
d) Điểm M và điểm Q nằm khác phía với điểm P, điểm P và điểm N nằm cùng phía với điểm M, điểm Q nằm giữa hai điểm P và N.
11 tháng 1 2017
Số điểm của Khanh là: 5+5+0+0+(-1)+(-1)=8(điểm). Số điểm của Minh là:10+5+5+(-1)+(-10)+(-10)=-1(điểm). Vậy Khanh có số điểm cao hơn.(vì 8 điểm>5điểm)
15 tháng 1 2017
Tổng số điểm bạn Sơn bắn được là:
3.5+0+2(-2)+2(-2)=7(điểm)
Tổng số điểm bạn Dũng bắn được là:
2.10+(-2)+3(-4)=6(điểm)
=> Sơn có điểm cao hơn
15 tháng 1 2017
Giải
Số điểm của Sơn la:
5 + 0 + (-2) = 3 (điểm).
Số điểm của Dung là:
10 + (-2) + (-4) = 4 (điểm).
Vì 4 điểm lớn hơn 3 điểm
Nên bạn Dùng được điểm cao hơn.
17 tháng 1 2020
Cố điểm của Sơn : \(5.3+0.1+\left(-2\right).2=11\) (đấu chấm là nhân)
Cố điểm của Dũng: \(10.2+\left(-2\right).1+\left(-4\right).3=6\)
CM
8 tháng 8 2017
Đáp án là C
Số đoạn thẳng tạo thành từ n điểm phân biệt trong đó không có ba điểm nào thẳng hàng là: n(n - 1)/2 (n ≥ 2; n ∈ N)
Theo đề bài có 28 đoạn thẳng được tạo thành nên ta có: n(n - 1)/2 = 28 ⇒ n(n - 1) = 56 = 8.7
Nhận thấy (n - 1) và n là hai số tự nhiên liên tiếp, suy ra n = 8.
23 tháng 5 2023
Chỗ kia chắc là \(n\) điểm chứ không phải \(n+1\) đâu.
Giả sử \(n\) điểm đã cho không thẳng hàng. Gọi S là tập hợp gồm \(n\) điểm đã cho và \(T=\left\{\left(A,B,C\right):A,B,C\in S|d\left(A,BC\right)>0\right\}\).
Vì n điểm đã cho không thẳng hàng nên \(T\ne\varnothing\). Mà T là có hữu hạn phần tử nên tồn tại phần tử \(\left(A,B,C\right)\in T\) sao cho \(d\left(A,BC\right)\) nhỏ nhất.
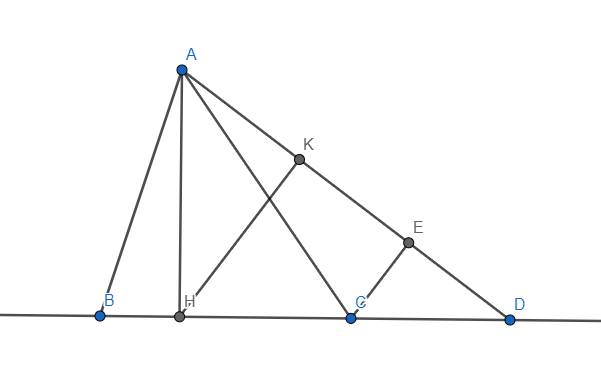
Theo giả thiết thì đường thẳng BC còn đi qua 1 điểm thứ ba nữa là \(D\in S\) . Không mất tính tổng quát, giả sử C nằm giữa B và D. Hạ \(AH\perp BC\), \(HK\perp AD\) và \(CE\perp AD\). Ta có \(CE< HK< AH\). Suy ra phần tử \(\left(C,A,D\right)\in T\) có \(d\left(C,AD\right)< d\left(A,BC\right)\), điều này là vô lí vì ta đã giả sử phần tử \(\left(A,B,C\right)\in T\) có \(d\left(A,BC\right)\) nhỏ nhất.
Vậy điều giả sử là sai, suy ra \(n\) điểm đã cho thẳng hàng.
22 tháng 5 2023
Vẫn như lần trước nhé bạn. Nếu bạn không xem được câu trả lời trên đây thì vào trong trang cá nhân của mình xem nhé.
KN
18 tháng 10 2020
có n điểm phân biệt (n>2,n thuộc N) cứ qua 2 điểm vẽ 1 đoạn thẳng thì vẽ được n.(n-1)
Theo bài ra ta có 300 đoạn thẳng nào có
n.(n-1) =300
n.(n-1) = 2.300
n.(n-1) =600
(n-1).n = 24.25 vì (n-1).n là tích của 28 số tự nhiên liên tiếp nên n =25