Mn giải giúp mình câu này với!
Cho tam giác ABC đều; hai đường trung tuyến BM, CN cắt nhau tại G. Gọi H là giao điểm của AG và BC
Chứng minh tam giác GBN = tam giác GBH.
Mình xin cảm ơn!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 9 2020
\(\widehat{ACD}=\widehat{BCD}-\widehat{BCA}=73-\left(90-\widehat{CBA}\right)=45\)=> Tam giác ACD vuông cân tại A=> AC=AD
Vẽ \(AH\perp DC\Rightarrow\hept{\begin{cases}AH//BE\\AH=DH=ACcos45=15\frac{\sqrt{2}}{2}sin62\end{cases}}\)
Xét \(AH//BE\Rightarrow\frac{EH}{DH}=\frac{AB}{AD}\Rightarrow\frac{EH}{AH}=\frac{AB}{AC}=cot62\Rightarrow EH=AHcot62=15\frac{\sqrt{2}}{2}sin62.cot62\)
\(=15\frac{\sqrt{2}}{2}cos62\)
Xét tam giác AHE vuông tại H \(\Rightarrow AE^2=AH^2+HE^2=\left(15\frac{\sqrt{2}}{2}\right)^2\left(sin^262+cos^262\right)=\left(15\frac{\sqrt{2}}{2}\right)^2\)
\(\Rightarrow AE=15\frac{\sqrt{2}}{2}cm\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
10 tháng 6 2023
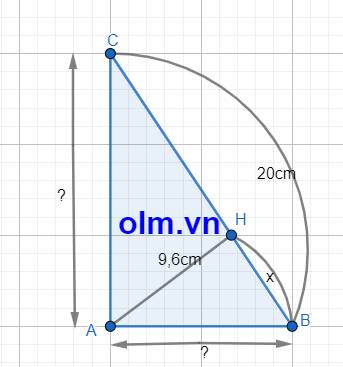
Gọi độ dài đoạn BH là: \(x\) ( cm) ; \(x\) > 0; AC > AB nên \(x\) < CH
Xét tam giác vuông HAB vuông tại H theo pytago ta có:
AB2 = HA2 + HB2 = 9,62 + \(x^2\) = 92,16 + \(x^2\)
Xét tam giác vuông AHC vuông tại H theo pytago ta có:
AC2 = HA2 + HC2 = 9,62 + (\(20-x\))2 = 92,16 + 400 - 40\(x\) + \(x^2\)
AC2 = 492,16 - 40\(x\) + \(x^2\)
Xét tam giác vuông ABC vuông tại A theo pytago ta có:
AC2 + AB2 = BC2
492,16 - 40\(x\) + \(x^2\) + 92,16 + \(x^2\) = 202
(\(x^2\) + \(x^2\)) - 40\(x\) + (492,16 + 92,16) - 400 = 0
2\(x^2\) - 40\(x\) + 584,32 - 400 = 0
2\(x^2\)- 40\(x\) + 184,32 =0
\(x^2\) - 20\(x\) + 92,16 = 0
△' = 102 - 92,16 = 7,84 > 0
\(x\)1 = -(-10) + \(\sqrt{7,84}\) = 12,8 ⇒ CH = 20 - 12,8 = 7,2 < BH (loại )
\(x_2\) = -(-10) - \(\sqrt{7,84}\) = 7,2 ⇒ CH = 20 - 7,2 = 12,8 (thỏa mãn)
Thay \(x_2\) = 7,2 vào biểu thức: AB2 = 92,16 + \(x^2\) = 92,16 + 7,22 = 144
⇒AB = \(\sqrt{144}\) = 12
Thay \(x_2\) = 7,2 vào biểu thức: AC2 = 492,16 - 40\(x\) + \(x^2\)
AC2 = 492,16 - 40\(\times\) 7,2 + 7,22 = 256
AC = \(\sqrt{256}\) = 16
Kết luận AB = 12 cm; AC = 16 cm
VN
6 tháng 4 2017
Hình khỏi vẽ đi ha.
c/ Xét tam giác ABH và tam giác ACH có:
góc BHA = góc CHA = 90 độ (gt)
góc ABH = góc HAC (vì tam giác AHC đồng dạng tam giác BAC)
=> tam giác ABH đồng dạng tam giác ACH (g.g)
=> HA/HC = HB/HA
=> HA.HA = HB.HC
=> HA^2 = HB.HC
Từ △ABC đều \(\Rightarrow AB=BC=CA;\hat{A}=\hat{B}=\hat{C}=60^{O}\)
Mà hai đường trung tuyến BM, CN cắt nhau tại G nên ta có: G là trọng tâm △ABC nên ta có: AG là trung tuyến BC
Mà NC là trung tuyến AB
Do đó: \(AN=NB=BH=HC=\frac{AB}{2}=\frac{BC}{2}\)
Xét △AMB và △BMC có:
AB = BC
AM = HC (cmt)
BM chung
=> △AMB = △BMC (ccc)
=> BM là tia phân giác góc B
Xét △GBN và △GBH có:
BG chung
\(\hat{NBG}=\hat{GBH}\) (BM là tia phân giác góc B)
BN = BH (cmt)
=> △GBN = △GBH (cgc)
1 lần nữa cảm ơn bạn nhé! <3