Cho hình bình hành ABCD ; góc BAD = 120 độ ; AB = 2 AD
a) CMR: Tia phân giác của góc ADC đi qua trung điểm E của AB .
b) Gọi F là trung điểm DC . CMR tam giác ADF đều và AD vuông góc với AC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bạn kiếm câu này ở đâu z mình đang luyện thi toán casio mà câu này khó quá bạn có biết chỉ mình

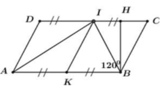
Kẻ BH là đường cao ứng với cạnh CD của hình bình hành ABCD
=> SABCD = BH.CD
Theo đề bài ta có chu vi hình bình hành ABCD bằng 60cm.
=> 2(AB + BC) = 60 ó 2.3BC = 60 ó BC = 10cm
Xét tứ giác KICB ta có:
IC = BC = KB = IK = 1 2 AB = 10cm
=> IKBC là hình thoi (dấu hiệu nhận biết).
Mà B ^ = 1200 => I C B ^ = 1800 – 1200 = 600
Xét tam giác ICB có: I C = B C I C B = 60 0
=> ICB là tam giác đều. (tam giác cân có góc ở đỉnh bằng 600).
=> BH vừa là đường cao vừa là đường trung tuyến ứng hay H là trung điểm của IC.
=> HI = HC = 1 2 BC = 5cm
Áp dụng định lý Pytago với tam giác vuông HBC ta có:
BH = B C 2 − H C 2 = 10 2 − 5 2 = 75 = 5 3 cm
=> SABCD = BH.AB = BH.2BC = 5 3 .2.10 = 100 3 cm2
Đáp án cần chọn là: A

Chiều cao là \(\dfrac{10+10}{2}=10\left(cm\right)\)
Diện tích hbh là \(10\cdot6=60\left(cm^2\right)\)

A B C D A' B' C' D' M N P Q E F
Lấy E là trung điểm A'D ; F là trung điểm BC'.
Dễ dàng chứng minh được \(\Delta EQM=\Delta FNP\left(c.g.c\right)\)
Từ đó suy ra \(MQ=NP\)
CMTT có \(MN=PQ\)
Do đó \(MNPQ\)là hình bình hành.
Vậy ...
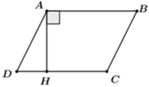
a, E là trung điểm của AB (gt) \(\Rightarrow AE=EB=\frac{1}{2}AB\)
\(AB=2AD\left(gt\right)\Rightarrow AD=\frac{1}{2}AB\)
Do đó: \(AE=AD\Rightarrow\Delta AED\) cân tại A \(\Rightarrow\widehat{AED}=\widehat{ADE}\) (tính chất tam giác cân) (1)
ABCD là hình bình hành(gt) \(\Rightarrow AB//CD\Rightarrow\widehat{AED}=\widehat{EDC}\) ( 2 góc so le trong ) (2)
Từ (1) và (2) \(\Rightarrow\widehat{ADE}=\widehat{EDC}\) mà tia DE nằm giữa 2 tia DA,DC \(\Rightarrow\)AE là tia phân giác của \(\widehat{ADC}\)
Vậy tia phân giác của \(\widehat{ADC}\) đi qua trung điểm E của AB.
b, ABCD là hình bình hành(gt) \(\Rightarrow AB=DC\)
F là trung điểm của DC (gt) \(\Rightarrow FD=FC=\frac{1}{2}DC=\frac{1}{2}AB=AD\)
Do đó: \(\Delta ADF\) cân tại D
\(AB//DC\left(cmt\right)\Rightarrow\widehat{BAD}+\widehat{ADF}=180^0\)
\(\Rightarrow120^0+\widehat{ADF}=180^0\) (vì \(\widehat{BAD}=120^0\) )
\(\Rightarrow\widehat{ADF}=60^0\)
Ta có: \(\Delta ADF\) cân tại D và \(\widehat{ADF}=60^0\left(cmt\right)\Rightarrow\Delta ADF\) đều
\(\Rightarrow AF=DF=AD\) \(\left(ĐN\right)\)
Mặt khác, DF = 1/2 DC nên AF = 1/2 DC
\(\Delta ADC\)có trung tuyến AF = 1/2 DC nên \(\Delta ADC\)vuông tại A
Vậy \(AD\perp AC.\)
Mong bạn hiêu bài và chúc bạn học tốt.