OLM ưu đãi đặc biệt gói SVIP 18 THÁNG dành cho nhà trường, đăng kí ngay!

OLM tuyển CTV cộng đồng hỏi đáp, đăng kí ngay!

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
PT
Pham Trong Bach
24 tháng 8 2019
Tọa độ giao điểm của hai đường thẳng  d 1 : x = 2 t y = - 1 + t  ; d2: x + 2y - 2 = 0 là: A. (0;-1) B. (2;0) C. (-1;0) D....
Đọc tiếp

Tọa độ giao điểm của hai đường thẳng  d 1 : x = 2 t y = - 1 + t  ; d2: x + 2y - 2 = 0 là:

A. (0;-1)

B. (2;0)

C. (-1;0)

D. (0;2)
#Hỏi cộng đồng OLM #Toán lớp 10
1
CM
Cao Minh Tâm
24 tháng 8 2019

Đáp án: B

Giả sử M là giao điểm của hai đường thẳng.

Đề kiểm tra 45 phút Hình học 10 Chương 3 có đáp án (Đề 4)

Đúng(0)
DT
Đinh Thuận
9 tháng 12 2018

tìm tọa độ giao điểm của các đường thẳng sau với Ox(d):=y=x-2 (d'):y=-x+2.Vẽ hai đường thẳng trên cùng mặt phẳng tọa dộ xác định toạn độ giao điểm của (d) và (d').Nhận xét gì về hai đường thẳng trên
#Hỏi cộng đồng OLM #Toán lớp 9
1
NL
Nguyễn Lê Phước Thịnh
4 tháng 12 2022

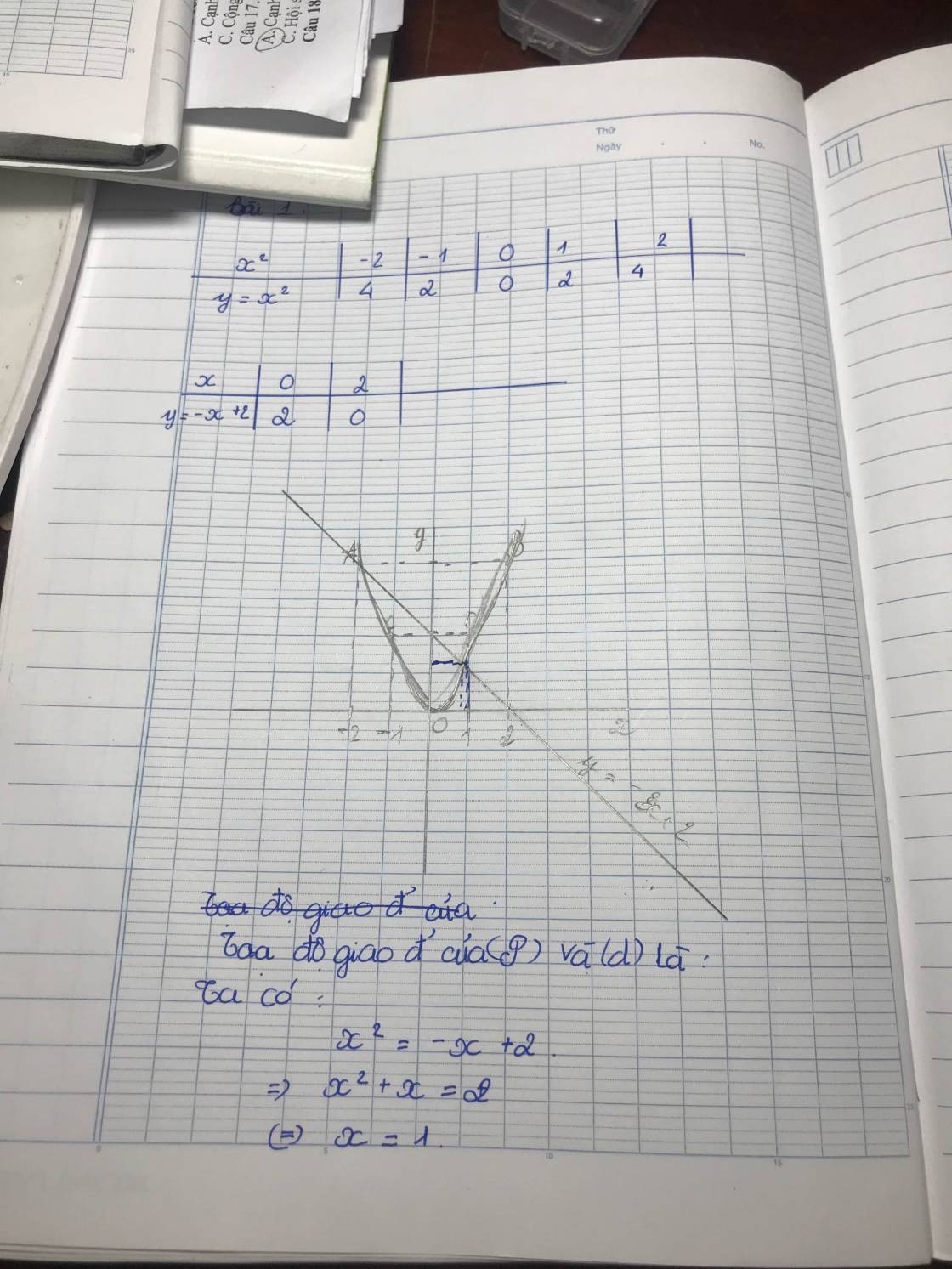
Tọa độ giao điểm là:

x-2=-x+2 và y=x-2

=>x=2 và y=0

Vì 1*(-1)=-1

nên (d) vuông góc với (d')

Đúng(0)
PT
Pham Trong Bach
11 tháng 4 2018
Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng d : x = 1 + t y = 2 + 3 t z ...
Đọc tiếp

Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng d : x = 1 + t y = 2 + 3 t z = 3 - t , d ' : x = 2 - 2 t ' y = - 2 + t ' z = 1 + 3 t '  . Tìm tọa độ giao điểm M của hai đường thẳng d và d’

A. M(-1;0;4)

B. M(4;0;-1)

C. M(0;4;-1)

D. M(0;-1;4)
#Hỏi cộng đồng OLM #Mẫu giáo
1
CM
Cao Minh Tâm
11 tháng 4 2018

Chọn D

Đúng(0)
DD
Đoàn Đức Hà
Giáo viên
16 tháng 2 2023 - olm

(2,5 điểm) Trong mặt phẳng tọa độ $Oxy$, cho parabol $(P): y=x^2$ và đường thẳng $(d):y=-x+2$. 

1. Tìm tọa độ giao điểm của $(P)$ và $(d)$. 

2. Gọi $A$, $B$ là hai giao điểm của $(P)$ và $(d)$. Tính diện tích tam giác $OAB$.
#Hỏi cộng đồng OLM #Toán lớp 9
3
XO
Xyz OLM
17 tháng 2 2023

Phương trình hoành độ giao điểm

x2 = -x + 2

<=> x2 + x - 2 = 0

Nhận thấy phương trình có a + b + c = 0 nên phương trình có 2 nghiệm \(x_1=1;x_2=-2\)

Với x1 = 1 => y1 = 1 => A(1,1) 

Với x2 = -2 => y2 = 4 => B(-2 , 4) 

Ta có BO = \(\sqrt{\left(-2\right)^2+4^2}=\sqrt{20}\);

\(OA=\sqrt{1^2+1^2}=\sqrt{2}\)

AB = \(\sqrt{3^2+3^2}=\sqrt{18}\)

Từ đó dễ thấy OA2 + AB2 = BO2 

=> Tam giác AOB vuông tại A

nên SAOB = \(\dfrac{\sqrt{18}.\sqrt{2}}{2}=3\)

x2 = -x + 2

<=> x2 + x - 2 = 0

Nhận thấy phương trình có a + b + c = 0 nên phương trình có 2 nghiệm 

Với x1 = 1 => y1 = 1 => A(1,1) 

Với x2 = -2 => y2 = 4 => B(-2 , 4) 

Ta có BO = ;

AB = 

Từ đó dễ thấy OA2 + AB2 = BO2 

=> Tam giác AOB vuông tại A

nên SAOB = 

Đúng(1)
BU
BAO UYEN8KT
14 tháng 3 2023

loading...  loading...  

Đúng(0)
LN
lu nguyễn
9 tháng 3 2019
1:cho hai điểm A(1;-4); B(1;2) viết pttq đường trung trực AB 2: cho tam giác ABC có A(1; 1); B(0; -2); C( 4;2). Viết phương trình tổng quát TRUNG TUYẾN CM 3: tìm tọa độ giao điểm của hai đường thẳng sau đây: \(\Delta1:\left\{{}\begin{matrix}x=22+2t\\y=55+5t\end{matrix}\right.\)và \(\Delta2:2x+3y-19=0\) 4:cho 4 điểm A(1; 2); B(-1; 4) C(2;2 ); D(-3; 2). Tìm tọa độ giao điểm của hai đường thẳng AB và CD 5: cho M(1;2) và đường thẳng...
Đọc tiếp

1:cho hai điểm A(1;-4); B(1;2) viết pttq đường trung trực AB

2: cho tam giác ABC có A(1; 1); B(0; -2); C( 4;2). Viết phương trình tổng quát TRUNG TUYẾN CM

3: tìm tọa độ giao điểm của hai đường thẳng sau đây: \(\Delta1:\left\{{}\begin{matrix}x=22+2t\\y=55+5t\end{matrix}\right.\)và \(\Delta2:2x+3y-19=0\)

4:cho 4 điểm A(1; 2); B(-1; 4) C(2;2 ); D(-3; 2). Tìm tọa độ giao điểm của hai đường thẳng AB và CD

5: cho M(1;2) và đường thẳng d: 2x+y-5=0. Tìm tọa độ của điểm đối xứng với điểm M qua d là?
#Hỏi cộng đồng OLM #Toán lớp 10
0
PT
Pham Trong Bach
5 tháng 10 2019
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d: x   =   1 + t y   =   2 + 3 ...
Đọc tiếp

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d: x   =   1 + t y   =   2 + 3 t z   =   3 - t  và d':  x   =   2 - 2 t ' y   = - 2 - t ' z   =   1 + 3 t '   . Tìm tọa độ M giao điểm của d và d'.
#Hỏi cộng đồng OLM #Toán lớp 12
1
CM
Cao Minh Tâm
5 tháng 10 2019

Chọn A

Đúng(0)
PT
Pham Trong Bach
25 tháng 3 2018
Tọa độ giao điểm của hai đường thẳng d: x - 3y - 1 = 0;  d ' = x = 2 t y = 3 - t  là: A. (1;4) B. (-1;4) C. (4;1) D. (4;-1)...
Đọc tiếp

Tọa độ giao điểm của hai đường thẳng d: x - 3y - 1 = 0;  d ' = x = 2 t y = 3 - t  là:

A. (1;4)

B. (-1;4)

C. (4;1)

D. (4;-1)
#Hỏi cộng đồng OLM #Toán lớp 10
1
CM
Cao Minh Tâm
25 tháng 3 2018

Đáp án: C

Gọi M là giao điểm của d và d’

Vì M ∈ d' ⇒ M(2t; 3-t)

Vì M ∈ d ⇒ 2t - 3.(3 - t) - 1 = 0 ⇔ 2t - 9 + 3t - 1 = 0 ⇔ t = 2 ⇒ M(4;1)

Đúng(0)
TC
Trần Công Thanh Tài
14 tháng 4 2022

Tìm tọa độ giao điểm của đường thẳng (d): \(\left\{{}\begin{matrix}x=2+t\\y=-1+3t\end{matrix}\right.\) (t ∈ R) với đường tròn (C):x2+y2-2x-1=0
#Hỏi cộng đồng OLM #Toán lớp 10
1
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 4 2022

Giao điểm của (d) và (C) thỏa mãn:

\(\left(2+t\right)^2+\left(-1+3t\right)^2-2\left(2+t\right)-1=0\)

\(\Leftrightarrow10t^2-4t=0\Rightarrow\left[{}\begin{matrix}t=0\\t=\dfrac{2}{5}\end{matrix}\right.\)

Vậy (d) và (C) cắt nhau tại 2 điểm có tọa độ là: \(\left[{}\begin{matrix}\left(2;-1\right)\\\left(\dfrac{12}{5};\dfrac{1}{5}\right)\end{matrix}\right.\)

Đúng(0)
HD
Hoài Dung
21 tháng 4 2020

Cho hai đường thẳng (d1): y = (2 + m)x + 1 và (d2): y = (1 +2m)x + 2

a) Tìm m để (d1) và (d2) cắt nhau.

b) Với m = -1, vẽ (d1) và (d2) trên cùng mặt phẳng tọa độ Oxy rồi tìm tọa độ giao điểm của 2 đường thẳng (d1) và (d2) bằng phép tính
#Hỏi cộng đồng OLM #Toán lớp 9
0
PT
Pham Trong Bach
14 tháng 4 2019
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng d: x = 1 - t y = 2 t z = 2 + ...
Đọc tiếp

Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng d: x = 1 - t y = 2 t z = 2 + 2 t , t ∈ ℝ  và mặt phẳng  (P): x + y -z -1 = 0 Giao điểm M của d và (P) có tọa độ là

A. M(1;0;2)

B. M(3;−4;−2)

C. M(0;2;4)

D. M(1;1;1)
#Hỏi cộng đồng OLM #Toán lớp 12
1
CM
Cao Minh Tâm
14 tháng 4 2019

Chọn B

Vậy M(3;−4;−2) là giao điểm của đường thẳng d và mặt phẳng (P).

Đúng(0)
NB
Nhok baka
29 tháng 3 2020

Cho parabol (P): y=x2 và đường thẳng (d): y=2x-m2+9

1. Tìm tọa độ các giao điểm của Parabol (P) và đường thẳng (d) khi m=1

2. Tìm (m) để đường thẳng (d) cắt parabol (P) tai hai điểm nằm về hai phía của trục tung
#Hỏi cộng đồng OLM #Toán lớp 9
1
AH
Akai Haruma
Giáo viên
29 tháng 3 2020

Lời giải:

1. PT hoành độ giao điểm:

$x^2-(2x-m^2+9)=0\Leftrightarrow x^2-2x+m^2-9=0(*)$

Khi $m=1$ thì pt trên trở thành: $x^2-2x-8=0$

$\Leftrightarrow (x-4)(x+2)=0\Rightarrow x=4$ hoặc $x=-2$

Khi $x=4\Rightarrow y=x^2=16$. Giao điểm thứ nhất là $(4,16)$

Khi $x=-2\Rightarrow y=x^2=4$. Giao điểm thứ hai là $(-2,4)$

2. $(P)$ và $(d)$ cắt nhau tại 2 điểm phân biệt $\Leftrightarrow (*)$ có 2 nghiệm phân biệt (hai nghiệm ấy chính là giá trị của 2 hoành độ giao điểm)

$\Leftrightarrow \Delta'=1-(m^2-9)>0\Leftrightarrow 10>m^2(1)$

Hai giao điểm nằm về phía của trục tung, nghĩa là 2 hoành độ giao điểm $x_1,x_2$ trái dấu. Điều này xảy ra khi $x_1x_2< 0\Leftrightarrow m^2-9< 0(2)$

Từ $(1);(2)$ suy ra $m^2-9< 0\Leftrightarrow -3< m< 3$

Đúng(1)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP