tìm "m" biết g(x)=m2^x+2mx-3=0 ; cho x=2 lsfm nghiệm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 11 2021
\(a,x^2-\left(2m-3\right)x+m^2=0-vô-ngo\)
\(\Leftrightarrow\Delta< 0\Leftrightarrow[-\left(2m-3\right)]^2-4m^2< 0\Leftrightarrow m>\dfrac{3}{4}\)
\(b,\left(m-1\right)x^2-2mx+m-2=0\)
\(m-1=0\Leftrightarrow m=1\Rightarrow-2x-1=0\Leftrightarrow x=-0,5\left(ktm\right)\)
\(m-1\ne0\Leftrightarrow m\ne1\Rightarrow\Delta'< 0\Leftrightarrow\left(-m\right)^2-\left(m-2\right)\left(m-1\right)< 0\Leftrightarrow m< \dfrac{2}{3}\)
\(c,\left(2-m\right)x^2-2\left(m+1\right)x+4-m=0\)
\(2-m=0\Leftrightarrow m=2\Rightarrow-6x+2=0\Leftrightarrow x=\dfrac{1}{3}\left(ktm\right)\)
\(2-m\ne0\Leftrightarrow m\ne2\Rightarrow\Delta'< 0\Leftrightarrow[-\left(m+1\right)]^2-\left(4-m\right)\left(2-m\right)< 0\Leftrightarrow m< \dfrac{7}{8}\)
CM
14 tháng 11 2017
Chọn D
Đặt t= x-1 hay x= t+1, thay vào pt đã cho ta được pt:
t2+ 2(1-m) t+ m2- 3 m+2= 0 (2)
Để pt (1) có nghiệm x≤ 1 khi và chỉ khi pt (2) có nghiệm t≤ 0
TH1: Pt(2) có nghiệm : t1≤ 0 ≤ t2
Khi đó; P= t1.t2 ≤0 hay m2- 3m+ 2≤ 0 hay 1≤ m ≤ 2
TH2: pt (2) có nghiệm
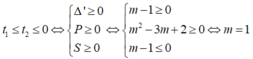
Kết luận: với 1≤ m≤ 2 thì pt (1) có nghiệm x≤1
TA
4 tháng 6 2021
PT có 2 nghiệm phân biệt `<=> \Delta'>0`
`<=>m^2-(m^2+m-5)>0`
`<=>-m+5>0`
`<=> m < 5`
Viet: `x_1+x_2=2m`
`x_1x_2=m^2+m-5`
Theo đề bài: `2(x_1^2+x_2^2)-3x_1x_2=29`
`<=>2[(x_1+x_2)^2-2x_1x_2]-3x_1x_2=29`
`<=>2(x_1+x_2)^2-7x_1x_2=29`
`<=>2.4m^2 - 7(m^2+m-5)=29`
`<=>` \(\left[{}\begin{matrix}m=6\left(L\right)\\m=1\left(TM\right)\end{matrix}\right.\)
Vậy `m=1`.
CM
16 tháng 1 2018
Chọn D
Đặt t= x-1 hay x= t+1, thay vào pt đã cho ta được pt:
t2+ 2(1-m) t+ m2- 3 m+2= 0 (2)
Để pt (1) có nghiệm x ≥ 1 khi và chi khi pt (2) có nghiệm t ≥ 0
+ TH1: Pt (2) có nghiệm t1 ≤ 0 ≤ t2
Khi đó; P= t1.t2 ≤ 0 hay m2- 3m+ 2 ≤ 0
Từ đó; 1≤ m≤ 2
+ TH2: Pt (2) có nghiệm :
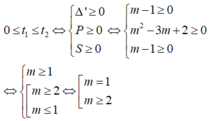
Kết luận: với 
thì pt (1) có nghiệm x ≥ 1
AH
Akai Haruma
Giáo viên
2 tháng 5 2023
Bài 1:
Gọi biểu thức trên là $P$
\(P=\frac{\sqrt{x}(\sqrt{x}-3)+3(\sqrt{x}+3)}{(\sqrt{x}+3)(\sqrt{x}-3)}.\frac{x-9}{\sqrt{x}-3}\)
\(=\frac{x+9}{(\sqrt{x}-3)(\sqrt{x}+3)}.\frac{(\sqrt{x}-3)(\sqrt{x}+3)}{\sqrt{x}-3}=\frac{x+9}{\sqrt{x}-3}\)
AH
Akai Haruma
Giáo viên
2 tháng 5 2023
Bài 2:
Để $(d)$ và $(d')$ song song với nhau thì:
$m^2-3=2m$
$\Leftrightarrow m^2-2m-3=0$
$\Leftrightarrow (m+1)(m-3)=0$
$\Leftrightarrow m+1=0$ hoặc $m-3=0$
$\Leftrightarrow m=-1$ hoặc $m=3$
26 tháng 8 2021
a: Ta có: \(\text{Δ}=\left(-2m\right)^2-4\cdot1\cdot\left(m+6\right)\)
\(=4m^2-4m-24\)
\(=4\left(m^2-m-6\right)\)
Để phương trình có hai nghiệm phân biệt thì Δ>0
\(\Leftrightarrow m^2-m-6>0\)
\(\Leftrightarrow\left(m-3\right)\left(m+2\right)>0\)
\(\Leftrightarrow\left[{}\begin{matrix}m>3\\m< -2\end{matrix}\right.\)
b: Ta có: \(\text{Δ}=\left(-2m\right)^2-4\cdot m\cdot\left(m+3\right)\)
\(=4m^2-4m^2-12m\)
=-12m
Để phương trình vô nghiệm thì Δ<0
hay m>0
c: Ta có: \(\text{Δ}=\left(2m-3\right)^2-4\left(m-2\right)\left(m+1\right)\)
\(=4m^2-12m+9-4\left(m^2-m-2\right)\)
\(=4m^2-12m+9-4m^2+4m+8\)
\(=-8m+17\)
Để phương trình có nghiệm kép thì Δ=0
hay \(m=\dfrac{17}{8}\)
Ta có:
\(g\left(x\right)=mx^2+2mx-3=0\)
Vì \(x=2\) là nghiệm của \(g\left(x\right)\) (gt).
+ Thay \(x=2\) vào \(g\left(x\right)\) ta được:
\(g\left(x\right)=m.2^2+2m.2-3=0\)
\(\Rightarrow m.4+4m-3=0\)
\(\Rightarrow4m+4m-3=0\)
\(\Rightarrow8m-3=0\)
\(\Rightarrow8m=0+3\)
\(\Rightarrow8m=3\)
\(\Rightarrow m=3:8\)
\(\Rightarrow m=\frac{3}{8}.\)
Vậy \(m=\frac{3}{8}.\)
\(g\left(x\right)=mx^2+2mx-3=0\)
Thay x = 2 vào biểu thức ta có : \(m.2^2+2m.2-3=0\Leftrightarrow4m+4m-3=0\Leftrightarrow8m-3=0\)
\(\Leftrightarrow8m=3\Leftrightarrow m=\frac{3}{8}\)