Cho các số nguyên a; b; c thỏa mãn: ab(a - b) + bc(b - c) + ca(c - a) = a + b + c. Chứng minh rằng a + b + c chia hết cho 27
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HC
22 tháng 7 2016
7+(-45)+159+(-243)+0,7=-121.3
7.(-45).159.(-243).0,7=8519458,5
3 tháng 2 2020
a) 225 = 3 mũ 2 nhân cho 5 mũ 2 => 225 chia hết cho các số nguyên tố : 3,5
b) 1800 = 2.3.5 mũ 2 . 7 => 1800 chia hết cho các số nguyên tố 2 , 3 , 5
c ) 1050 = 2.3.5 mũ 2 . 7 => 1050 chia hết cho các số nguyên tố 2,3,5,6
d) 2060 = 2 mũ 2 . 3 mũ 2 . 5. 17 => 3060 chia hết cho các số nguyên tố 2,3,5,17
3 tháng 2 2020
225 = 32 * 52
1800 = 23 * 32 * 52
1050 = 2 * 3 * 52 * 7
3060 = 22 * 32* 5 *17
CM
6 tháng 12 2017
Chọn D.
Ta có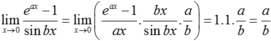 
Vậy để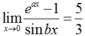 
thì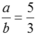 
. Vì a và b là các số nguyên dương nên suy ra a = 5k, b = 3k với k nguyên dương. Do đó ab = 15k2.
+ 15k2 = 15 ⇔ k2 = 1 ⇒ k = 1 ⇒ ab = 15.
+ 15k2 = 60 ⇔ k2 = 4 ⇒ k = 2 ⇒ ab = 60.
+ 15k2 = 240 ⇔ k2 = 16 ⇒ k = 4 ⇒ ab = 240.
Vậy cả ba đáp án đều đúng.
CM
15 tháng 8 2019
a) Đ
b) S
Vì tổng của hai số nguyên bằng 0 thì cả hai số nguyên đó đều bằng 0 hoặc hai số đó là hai số đối nhau. Ví dụ: (-3) + 3 = 0+ 0 = 0
c) Đ
d) S
Vì khẳng định sẽ bị sai khi các số nguyên đó không cùng dấu.
22 tháng 1 2016
a,-25;-19;2;4;I-5I
b,I2I=2;II-5II=5;I-25I=25;I-19I=19;I4I=4
c2xI-5Ix-25x-19x4=19000
22 tháng 1 2016
a; -25,-19,2,4,(-5) thông cảm ko có trị tuyệt đối
b;(2)=2;(-5)=5;(-25)=25;(-19)=19;(4)=4
c; 19000
tich di