1) Chứng minh: x-x2-3<0 với mọi x
2) Cho a=111...1(2n chữ số 1); b=444...4 (n chữ số 4). Chứng minh a+b+1 là 1 số chính phương
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do \(x_1< x_2\). Do đó: \(x_1=\frac{2n-1-1}{2}=n-1\) và \(x_2=\frac{2n-1+1}{2}=n\)
Ta có \(x_1^2-2x_2+3=\left(n-1\right)^2-2n+3\)
\(=n^2-2n+1-2n+3=n^2-4n+4=\left(n-2\right)^2\ge0\)
Dấu "=" xảy ra <=> n=2

2. -x2 + x - 33 = -x2 + x - 1/4 - 131/4 = -( x2 - x + 1/4 ) - 131/4 = -( x - 1/2 )2 - 131/4
-( x - 1/2 )2 ≤ 0 ∀ x => -( x - 1/2 )2 - 131/4 ≤ -131/4 < 0 ∀ x ( đpcm )
3. x2 + 4x + 33 = x2 + 4x + 4 + 29 = ( x + 2 )2 + 29
( x + 2 )2 ≥ 0 ∀ x => ( x + 2 )2 + 29 ≥ 29 > 0 ∀ x ( đpcm )
4. x2 + 8x = x2 + 8x + 16 - 16 = ( x + 4 )2 - 16
( x + 4 )2 ≥ 0 ∀ x => ( x + 4 )2 - 16 ≥ -16 ∀ x
Đẳng thức xảy ra <=> x + 4 = 0 => x = -4
Vậy GTNN của biểu thức = -16, đạt được khi x = -4

\(\Delta'=\left(a-1\right)^2-2a+5=a^2-4a+6=\left(a-2\right)^2+2>0\) \(\forall a\)
\(\Rightarrow\) Phương trình đã cho luôn có 2 nghiệm pb
Theo Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(a-1\right)\\x_1x_2=2a-5\end{matrix}\right.\)
\(x_1< 1< x_2\Leftrightarrow\left(x_1-1\right)\left(x_2-1\right)< 0\)
\(\Leftrightarrow x_1x_2-\left(x_1+x_2\right)+1< 0\)
\(\Leftrightarrow2a-5-2\left(a-1\right)+1< 0\)
\(\Leftrightarrow-2< 0\) (luôn đúng)
Vậy với mọi a thì pt luôn có 2 nghiệm thỏa mãn \(x_1< 1< x_2\)

a, x2 - 2x + 3 = x2 - 2x + 1 + 2 = (x - 1)2 + 2
Mà (x - 1)2 > hoặc = 0 => (x - 2)2 + 2 > 0 với mọi x

Ta có :
\(x^2-4x+5=\left(x^2-2.2x+2^2\right)+1=\left(x-2\right)^2+1\ge1>0\)
Vậy đa thức \(x^2-4x+5\) vô nghiệm với mọi giá trị của x
Chúc bạn học tốt ~

\(x^{2^{ }}+2\left(m-1\right)x-6m-7=0\left(1\right)\)
a) \(Dental=\left[2\left(m-1\right)\right]^2-4\cdot1\cdot\left(-6m-7\right)\)
\(< =>4\cdot\left(m^2-2m+1\right)+24m+28\)
\(< =>4m^2-8m+4+24m+28\)
\(< =>4m^2+16m+32\)
\(< =>\left(2m+4\right)^2+16>0\) với mọi m
Vậy phương (1) luôn có 2 nghiệm phân biệt với mọi m
b) Theo định lí vi ét ta có:
x1+x2= \(\dfrac{-2\left(m-1\right)}{1}=-2m+1\)
x1x2= \(-6m-7\)
quy đồng
khử mẫu
tách sao cho có tích và tổng
thay x1x2 x1+x2
kết luận
mặt xấu vl . . .![]()

Ta có:
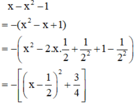
Ta có: 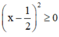 với mọi số thực x
với mọi số thực x
⇒ 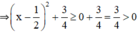 với mọi số thực x
với mọi số thực x
⇒ 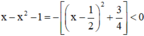 với mọi số thực (ĐPCM)
với mọi số thực (ĐPCM)