Question

[Pham Trong Bach]

Cho phương trình ax + by = c với a $\ne$0; b  $\ne$ 0. Nghiệm của phương trình được biểu diễn bởi.

A.  $\left\{\begin{array}{l}x\in R\\ y=-\frac{a}{b}x+\frac{c}{b}\end{array}\right.$

B.  $\left\{\begin{array}{l}x\in R\\ y=-\frac{a}{b}x-\frac{c}{b}\end{array}\right.$

C.  $\left\{\begin{array}{l}x\in R\\ y=\frac{c}{b}\end{array}\right.$

D.  $\left\{\begin{array}{l}x\in R\\ y=-\frac{c}{b}\end{array}\right.$

Answer 1

[Cao Minh Tâm]

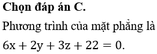
Ta có với a ≠  0; b ≠  0 thì ax + by = c ⇔  by = −ax + c  ⇔ y = − a b x + c b

Nghiệm của phương trình được biểu diễn bởi  x ∈ R y = − a b x + c b

Đáp án: A