Cho 1/a=1/2(1/a+1/b) (với a,b,c\(\ne\)0; b\(\ne\)c) chứng minh rằng a/b =a-c/c-b
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Từ \(\frac{1}{c}=\frac{1}{2}\left(\frac{1}{a}+\frac{1}{b}\right)\Rightarrow\frac{1}{c}=\frac{1}{2}\left(\frac{a+b}{ab}\right)\)
\(\Rightarrow\frac{1}{c}=\frac{a+b}{2ab}\)
\(\Rightarrow2ab=c.\left(a+b\right)\)
\(\Rightarrow ab+ab=ac+bc\)
\(\Rightarrow ab-bc=ac-ab\)
\(\Rightarrow b.\left(a-c\right)=a.\left(c-b\right)\)
\(\Rightarrow\frac{a}{b}=\frac{a-c}{c-b}\)

\(\frac{1}{c}=\frac{1}{2}\left(\frac{1}{a}+\frac{1}{b}\right)\)
\(\frac{1}{c}:\frac{1}{2}=\frac{1}{a}+\frac{1}{b}\)
\(\frac{2}{c}=\frac{a+b}{ab}\)
\(\Rightarrow2ab=ac+bc\)
\(\Rightarrow ac-ab=ab-bc\)
\(\Rightarrow a.\left(c-b\right)=b.\left(a-c\right)\)
\(\Rightarrow\frac{a}{b}=\frac{a-c}{c-b}\)( đpcm )

\(\sqrt{\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}}=\sqrt{\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}+\frac{2\left(a+b+c\right)}{abc}}\)
\(=\sqrt{\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}+\frac{2}{ab}+\frac{2}{bc}+\frac{2}{ca}}\)
\(=\sqrt{\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)^2}=\left|\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right|\)

\(\sqrt{\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}}=\sqrt{\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}+\frac{2\left(a+b+c\right)}{abc}}\) ( do \(a+b+c=0\) )
\(=\sqrt{\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}+\frac{2}{ab}+\frac{2}{bc}+\frac{2}{ca}}\)
\(=\sqrt{\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)^2}\)
\(=\left|\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right|\) ( đpcm )

2: \(A=9^n\cdot81-9^n+3^n\cdot9+3^n\)
\(=9^n\cdot80+3^n\cdot10\)
\(=10\left(9^n\cdot8+3^n\right)⋮10\)

Áp dụng tỉ dãy số bằng nhau. Ta có:
\(\frac{1}{c}=\frac{1}{2}\left(\frac{1}{a}+\frac{1}{b}\right)\Leftrightarrow\frac{1+1+1}{a+b+c}=1\)
\(\Rightarrow a=b=c\)
\(\Rightarrow\frac{a}{b}\Leftrightarrow1-1\Leftrightarrow0\)
\(\Rightarrow PT=\frac{a-c}{c-b}=\frac{\left(a-c\right)^0}{\left(c-b\right)^0}=0\)
Vậy dấu = xảy ra khi a - c = a , c - b = b
Ta có ĐPCM
Ps: Chả biết đúng hay không nữa
như này mới đúng nè
ta có\(\frac{1}{c}=\frac{1}{2}\left(\frac{1}{a}+\frac{1}{b}\right)\)
\(\Rightarrow\frac{1}{a}+\frac{1}{b}=\frac{1}{c}.2\)
\(\Rightarrow\frac{b}{ab}+\frac{a}{ba}=\frac{2}{c}\)
\(\Rightarrow\frac{b+a}{ab}=\frac{2}{c}\)
\(\Rightarrow\left(b+a\right)c=2ab\)
\(\Rightarrow cb+ca=ab+ab\)
\(\Rightarrow ca-ab=ab-cb\)
\(\Rightarrow b\left(a-c\right)=a\left(c-b\right)\)
\(\Rightarrow\frac{a-c}{c-b}=\frac{a}{b}\)

Ta có: \(\sqrt{\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}}\)
\(=\sqrt{\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}-2\left(\dfrac{c}{abc}+\dfrac{b}{abc}+\dfrac{a}{abc}\right)}\)
\(=\sqrt{\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}-2\cdot\dfrac{a+b+c}{abc}}\)
\(=\sqrt{\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)^2}=\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\)
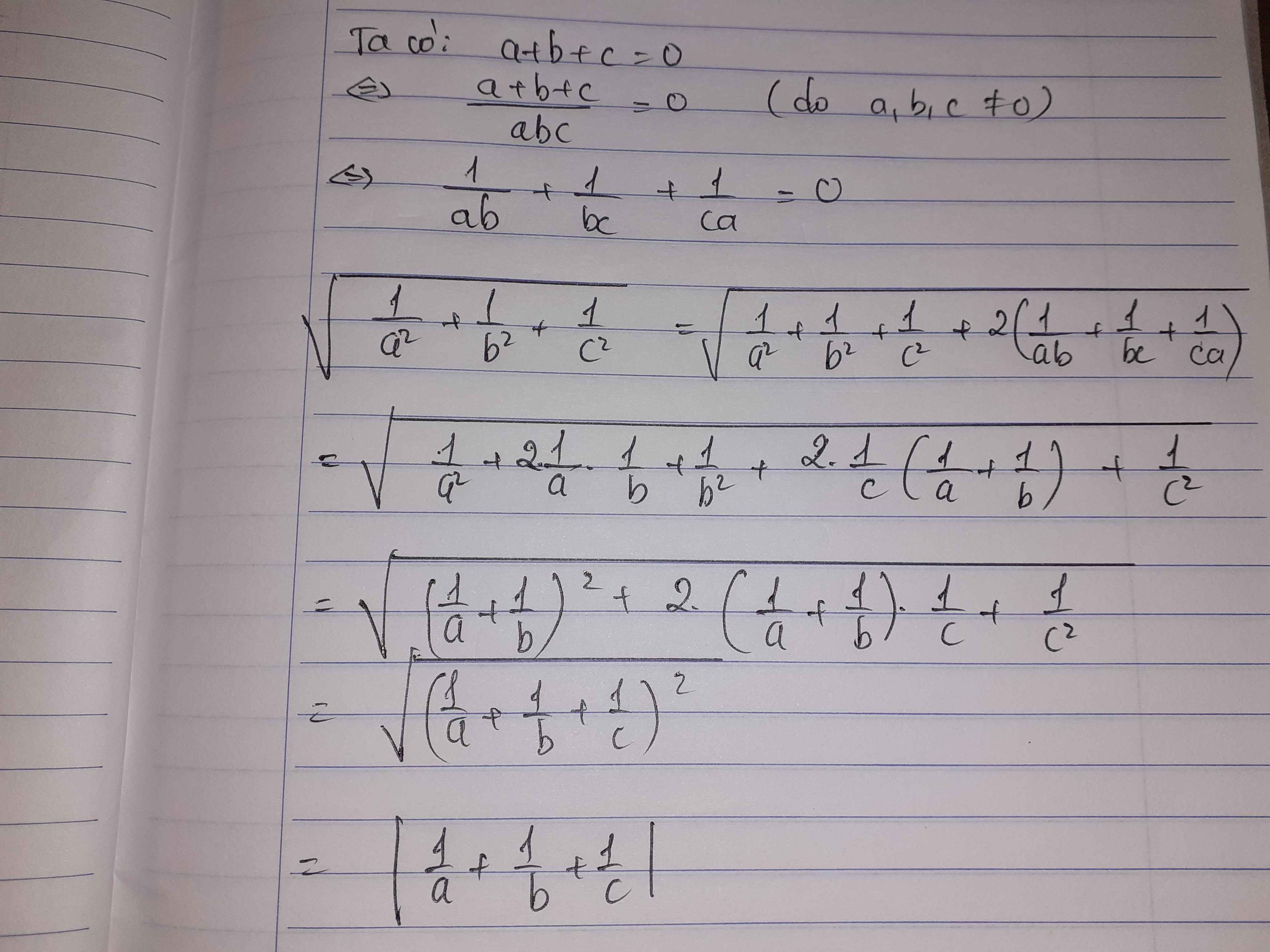
Ta có: 1/c = 1/2(1/a+1/b) <=> 1/c:1/2 = 1/a+1/b
<=> 1/c.2/1 = (a+b)/ab
<=> 2/c = (a+b)/ab
<=> 2ab = ac + bc (1).
Lại có: a/b=a-c/c-b <=> a(c-b) = b(a-c)
<=> ac – ab = ab – bc
<=> 2ab = ac + bc (2).
Từ (1) và (2) => a/b=a-c/c-b (đpcm)