Cho U1=1; Un= √3 + Un-1 / 1 - √3 Un-1
Tính U8
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 1 2021
\(u_1+u_4=u_2+u_3\) , mà \(u_1+u_2+u_3+u_4=20\)
\(\Rightarrow u_1+u_4=u_2+u_3=10\)
\(\Rightarrow2u_1+3d=10\)
\(\dfrac{u_1+u_4}{u_1u_4}+\dfrac{u_2+u_3}{u_2u_3}=\dfrac{25}{24}\Leftrightarrow10\left(\dfrac{1}{u_1u_4}+\dfrac{1}{u_2u_3}\right)=\dfrac{25}{24}\)
\(\Leftrightarrow\dfrac{1}{u_1\left(u_1+3d\right)}+\dfrac{1}{\left(u_1+d\right)\left(u_1+2d\right)}=\dfrac{5}{48}\)
\(\Leftrightarrow\dfrac{1}{u_1\left(10-u_1\right)}+\dfrac{9}{\left(10+u_1\right)\left(20-u_1\right)}=\dfrac{5}{48}\)
\(\Leftrightarrow\dfrac{5\left(u_1-8\right)\left(u_1-2\right)\left(u_1^2-10u_1-120\right)}{48u_1\left(u_1-20\right)\left(u_1^2-10\right)}=0\)
Nhiều nghiệm quá
CM
30 tháng 1 2017
Ta có u 2 = 1 3
Với n ≥ 3 ta có
u 1 + 2 u 2 + . . + n - 1 u n - 1 + n u n = n n 2 - 1 u n + n u n = n 3 u n ⇒ n u n 3 = n u n + n - 1 3 u n - 1 ⇒ u n u n - 1 = n - 1 3 n 3 - n = n - 1 n 2 n n + 1 1
Từ (1) suy ra
u n u 2 = u n u n - 1 . u n - 1 u n - 2 . . . u 3 u 2 = n - 1 n 2 . n - 1 n - 2 2 . . 2 3 2 n n - 1 . n - 1 n . . . 3 4 = 12 n 2 n + 1 ⇒ u n = 4 n 2 n + 1
Vậy l i m n + 2018 3 U n = 4
Đáp án D
CM
1 tháng 11 2019
Chọn B.
Phương pháp:
Công thức tính tổng n số hạng đầu tiên của cấp số cộng có số hạng đầu u1 và công sai d
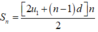
Cách giải:
Ta có: u n + 1 = u n + 2 , ∀ n ∈ ℕ *
⇒ ( u n ) là cấp số cộng có u 1 = - 5 , d = 2
10 tháng 3 2021
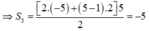
Công sai \(d=\dfrac{u_{2020}-u_1}{2019}=\dfrac{3333}{673}\).
Ta có \(d.S_n=\dfrac{u_2-u_1}{\sqrt{u_1}+\sqrt{u_2}}+\dfrac{u_3-u_2}{\sqrt{u_2}+\sqrt{u_3}}+...+\dfrac{u_{2020}-u_{2019}}{\sqrt{u_{2019}}+\sqrt{u_{2020}}}=\sqrt{u_2}-\sqrt{u_1}+...+\sqrt{u_{2020}}-\sqrt{u_{2019}}=\sqrt{u_{2020}}-\sqrt{u_1}=100-1=99\)
\(\Rightarrow S_n=\dfrac{99}{d}=\dfrac{2019}{101}\).
Toán hay Vật lí zậy ???