Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = 2a; và góc giữa đường thẳng AB và mặt phẳng (SBC) bằng . Tính thể tích V của khối chóp đã cho.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi O, I lần lượt là trung điểm của AC, SC.
Ta có:
∆ A B C vuông cân tại B ⇒ O là tâm đường tròn ngoại tiếp và A C = A B 2 = a 2 .
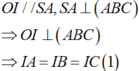
∆ S A C vuông tại A, I là trung điểm của S C ⇒ I S = I C = I A 2
Từ (1), (2) suy ra I là tâm mặt cầu ngoại tiếp hình chóp S.ABC, bán kính
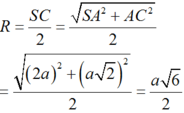
Chọn: A

Đáp án là D
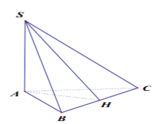
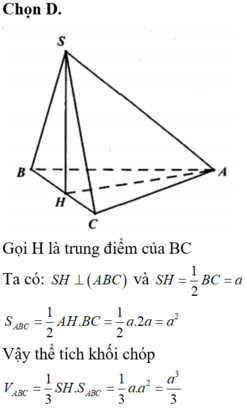
Gọi H là trung điểm của BC, ta có: AH ⊥ BC
Do SA
⊥
(ABC) ![]()
Ta có: ![]()
Xét tam giác vuông SAH:
![]()
![]()

Đáp án là B
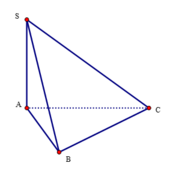
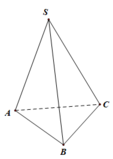
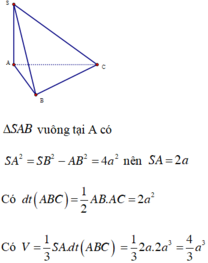
Tam giác SAB vuông tại A có S A 2 = S B 2 - A B 2 = 4 a 2 nên SA= 2a
Có S A B C = 1 2 A B . A C = 2 a 2
Có V = 1 3 S A . S A B C = 4 a 3 3

Đáp án B.
Dựng tam giác đều IAB (I và C cùng phía bờ AB).
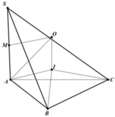
Ta có:
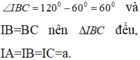
Qua I dựng đường thẳng song song với SA, cắt đường trung trực của SA tại O thì O là tâm mặt cầu ngoại tiếp hình chóp.
Gọi M là trung điểm của SA.
Ta có:
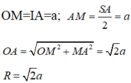

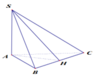


Đáp án là B
Gọi H, K, M lần lượt là trung điểm của AC, BC, SB và vì tam giác ABC vuông tại B suy ra HK ⊥ BC (1)
Gọi E là hình chiếu của H trên mặt phẳng (SBC) => HE ⊥ BC(2).
Từ (1), (2) suy ra EK ⊥ BC => EK ≡ MK( vì MK ⊥ BC) do đó
Lại có HA = HB = HC, MA = MB = MC ( do M là tâm mặt cầu ngoại tiếp S.ABC) suy ra MH là trục của đường tròn ngoại tiếp tam giác ABC suy ra ∆ MHK vuông tại H => MH = tan30 ° . H K = a 3 .
Vậy thể tích khối chóp