Cho hình bình hành MNPQ có ME \(\perp\) PQ ở E; PF \(\perp\) MN ở F.
Chứng minh: a, MP=EF.
b, MP, NQ, EF đồng quy.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 8 2018
Diện tích hình thoi ABCD hay diện tích hình bình hành MNPQ là:
18 x 16 : 2 = 144 (cm2)
Chiều cao của hình bình hành MNPQ là:
144 : 9 = 16 (cm)
Đáp số: 16 cm
23 tháng 12 2021
a: Xét tứ giác MNEP có
H là trung điểm của NP
H là trung điểm của ME
Do đó: MNEP là hình bình hành
b: Ta có: MNEP là hình bình hành
=>MN//PE
mà QP//MN
và PE,QP có điểm chung là P
nên E,P,Q thẳng hàng
29 tháng 10 2021
Theo mình thì mình nghĩ nó là chứng minh ENFQ là hình bình hành. Nếu sai thì rất xin lỗi bạn.
Giải
Ta có: \(\hept{\begin{cases}EN=\frac{1}{2}MN\\QF=\frac{1}{2}QP\end{cases}}\)(vì E là trung điểm MN và F là trung điểm QP)
Mà \(MN=QP\)(vì MNPQ là hình bình hành)
Nên \(EN=QF\left(1\right)\)
Lại có: \(MN//PQ\)(vì MNPQ là hình bình hành)
Do đó \(EN//QF\left(2\right)\)
CM
25 tháng 1 2018
Đáp án B
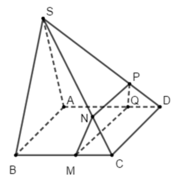
Ta có: MN // BS ⇒ C M C B = C N C S
MQ // CD // AB (do ABCD là hình bình hành nên AB //CD) ⇒ C M C B = D Q D A
NP // CD ⇒ C N C S = D P D S
Do đó: D P D S = D Q D A PQ // SA (Định lý Ta - lét trong tam giác SAD)
Lại có MN // BS và SB ∩ SA = S
Do đó MN không thể song song với PQ
Xét tứ giác MNPQ có NP // MQ (//CD)
Do đó MNPQ là hình thang.
Vậy khẳng địn (1) và (3) đúng.
Đáp án B
7 tháng 10 2021
Xét ΔMQN có
E là trung điểm của MN
H là trung điểm của MQ
Do đó: EH là đường trung bình của ΔMQN
Suy ra: EH//NQ và \(EH=\dfrac{NQ}{2}\left(1\right)\)
Xét ΔQPN có
F là trung điểm của NP
G là trung điểm của GP
Do đó: FG là đường trung bình của ΔQPN
Suy ra: FG//NQ và \(FG=\dfrac{NQ}{2}\left(2\right)\)
Từ (1)và (2) suy ra EH//GF và EH=GF
hay EHGF là hình bình hành
