Cho tam giác ABC vuông tại A, trung tuyến AM. Biết AB = 5cm, AC = 12 cm, khi đó độ dài trung tuyến AM là:(1 Point)6,5 cm6 cm5 cm13 cm2Cho tứ giác ABCD, gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Để tứ giác MNPQ là hình chữ nhật khi đó tứ giác ABCD cần thêm điều kiện là:(1 Point)AC ⊥ BDAB = CDAC = BDAD = AB3Cho hình thang cân ABCD (AB // CD) , biết CD = 12cm, AB = 6cm, AD = 5cm. Khi đó độ dài đường cao...
Đọc tiếp
Cho tam giác ABC vuông tại A, trung tuyến AM. Biết AB = 5cm, AC = 12 cm, khi đó độ dài trung tuyến AM là:
(1 Point)
6,5 cm
6 cm
5 cm
13 cm
2
Cho tứ giác ABCD, gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Để tứ giác MNPQ là hình chữ nhật khi đó tứ giác ABCD cần thêm điều kiện là:
(1 Point)
AC ⊥ BD
AB = CD
AC = BD
AD = AB
3
Cho hình thang cân ABCD (AB // CD) , biết CD = 12cm, AB = 6cm, AD = 5cm. Khi đó độ dài đường cao hình thang là:
(1 Point)
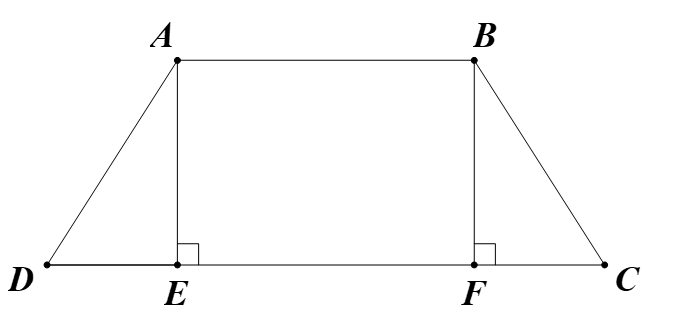
3 cm
4,5 cm
4 cm
4
Trong các hình vẽ đưới đây, tứ giác là hình bình hành là:
(1 Point)
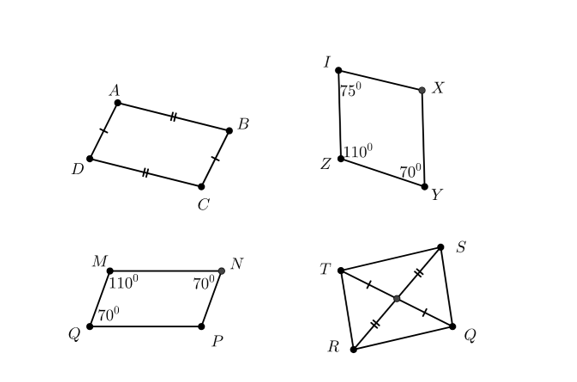
Tứ giác ABCD, tứ giác IXYZ, tứ giác MNPQ.
Tứ giác ABCD, tứ giác MNPQ, tứ giác TSQR.
Tứ giác ABCD, tứ giác MNPQ.
Cả 4 tứ giác.
5
Cho hình vẽ sau: biết góc ADE = 73 độ, góc ABC = 73 độ , D là trung điểm của AB, AE = 6cm. Khi đó độ dài AC là:
(1 Point)
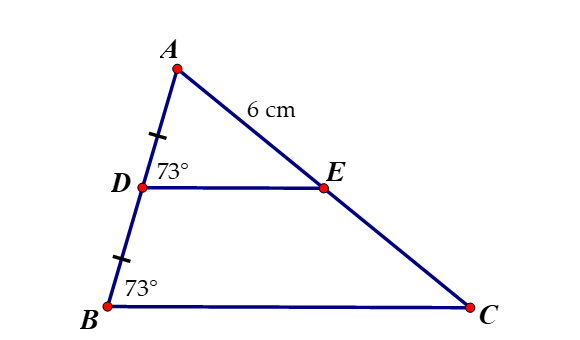
6 cm
9 cm
12 cm
6
Chọn khẳng định SAI trong các khẳng định sau:
(1 Point)
Đường thẳng đi qua trung điểm 2 cạnh đáy của hình thang là trục đối xứng của hình thang.
Tam giác đều có 3 trục đối xứng
Trục đối xứng của tam giác cân là đường thẳng chứa đường trung tuyến ứng với cạnh đáy của tam giác.
Đường tròn có vô số trục đối xứng
7
Chọn khẳng định SAI trong các khẳng định sau:
(1 Point)
Hình thang có 1 góc vuông là hình chữ nhật.
Hình bình hành có 2 đường chéo bằng nhau là hình chữ nhật.
Hình bình hành có 1 góc vuông là hình chữ nhật.
Tứ giác có 3 góc vuông là hình chữ nhật.
8
Cho hình thang ABCD (AB // CD), biết , AM và BM là các tia phân giác của các góc A và B của hình thang (M thuộc CD). Khi đó chu vi của hình thang ABCD là:
(1 Point)
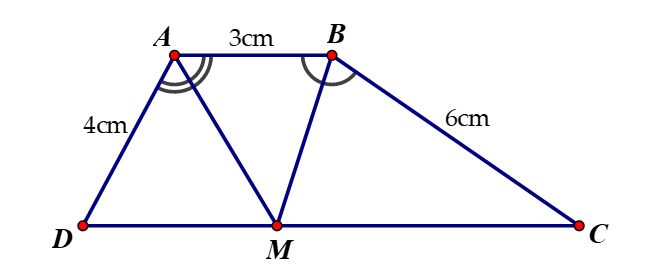
24 cm
22 cm
23 cm
9
Trong các hình vẽ sau đây, tứ giác là hình thang cân là:
(1 Point)
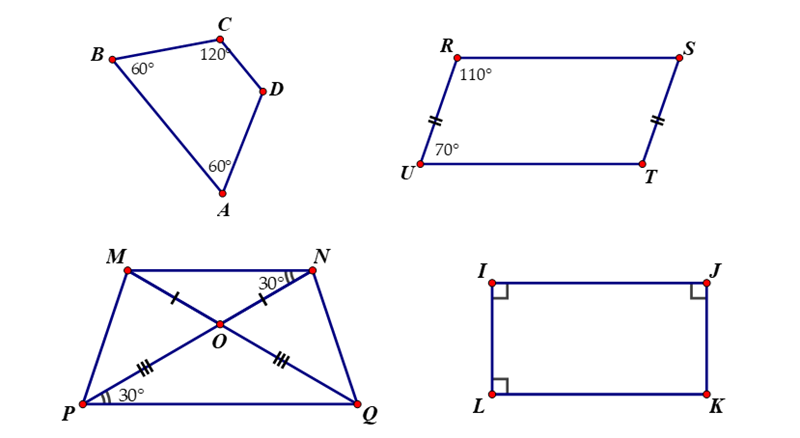
Tứ giác ABCD, tứ giác MNQP, tứ giác RSTU
Tứ giác ABCD, tứ giác IJKL, tứ giác MNQP
Cả 4 tứ giác
Tứ giác ABCD, tứ giác MNQP
10
Trong các khẳng định sau, khẳng định nào SAI:

(1 Point)
2 điểm M và N đối xứng với nhau qua điểm O khi O là trung điểm của MN.
Hai tam giác đối xứng qua 1 điểm thì bằng nhau.
Hình bình hành có 1 tâm đối xứng.
Tâm đối xứng của tam giác đều là trọng tâm của tam giác
Submit








Ta có BC = 2 AM = 13
Tam giác BAN vuông tại A nên AB2 + AN2 = BN2 = 61, (1)
Tương tự AB2 + AC2 = 132=169, (2)
Trừ vế với vế của (2) cho (1) ta được: AB2 + AC2 - AB2 - AN2 = 169-61=8 hay AC2 - AN2 =8
Do AC = 2AN nên 4AN2 - AN2 = 3AN2 = 8 hay AN2 = 8/3 hay AN = 2\(\sqrt{\frac{2}{3}}\)
Vậy AC = 4\(\sqrt{\frac{2}{3}}\)
AB = \(\sqrt{BC^2-AC^2}\)
Làm sao tính được BC = 13 vậy bạn?