Question

[Incognito]

Cho hình vuông ABCD nội tiếp đường tròn (O;R). Điểm E di động trên cung nhỏ CD. AE cắt BD,CD theo thứ tự ở M,N; BE cắt AC,CD theo thứ tự ở P,Q. Hai đoạn DP và CM cắt nhau tại I.

a) Chứng minh: \(DM.CE=\sqrt{2}.OM.ED\) ?

b) Tìm vị trí điểm E trên cung nhỏ DC sao cho biểu thức \(\frac{OM}{DM}+\frac{OP}{CP}\) đạt GTNN ?

c) Chứng minh: S_DPQ = S_CMN và \(\frac{IM}{ME}+\frac{NQ}{AB}+\frac{IP}{PE}=1\) ?

Answer 1

[Nguyễn Tất Đạt]

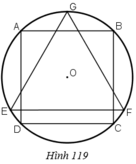
A B C D O M N P Q E I

a) Ta có: \(\Delta\)ABC vuông cân tại B (Vì tứ giác ABCD là hình vuông)

Theo tỉ số lượng giác :  \(AC=AB\sqrt{2}\Rightarrow\frac{1}{AB}=\frac{\sqrt{2}}{AC}\Leftrightarrow\frac{AM}{AB}=\frac{AM\sqrt{2}}{AC}\) (1)

Dễ thấy \(\Delta\)AMB ~ \(\Delta\)DME (g.g) \(\Rightarrow\frac{AM}{AB}=\frac{DM}{DE}\) (2)

Lại có: ^AEC = 90⁰ và AC vuông góc BD nên \(\Delta\)AOM ~ \(\Delta\)AEC (g.g) \(\Rightarrow\frac{AM}{AC}=\frac{OM}{CE}\)(3)

Thế (2) và (3) vào (1) ta có hệ thức: \(\frac{DM}{DE}=\frac{OM\sqrt{2}}{CE}\Rightarrow DM.CE=\sqrt{2}.OM.DE\)(đpcm).

b) Áp dụng BĐT AM-GM cho 2 số không âm: \(\frac{OM}{DM}+\frac{OP}{CP}\ge2\sqrt{\frac{OM}{DM}.\frac{OP}{CP}}\)

Từ kết quả câu a ta rút ra: \(\frac{OM}{DM}=\frac{CE}{\sqrt{2}.DE}\). Suy ra: \(\frac{OM}{DM}+\frac{OP}{CP}\ge2\sqrt{\frac{1}{\sqrt{2}}.\frac{CE}{CP}.\frac{OP}{DE}}\)(*)

Ta có các cặp tam giác đồng dạng sau (TH g.g): \(\Delta\)ABP ~ \(\Delta\)ECP và \(\Delta\)BOP ~ \(\Delta\)BED 

\(\Rightarrow\frac{CE}{CP}=\frac{AB}{BP}=\frac{R\sqrt{2}}{BP}\) (4) và \(\frac{OP}{DE}=\frac{BP}{BD}=\frac{BP}{2R}\) (5)

Thế (4), (5) vào (*) ta được: \(\frac{OM}{DM}+\frac{OP}{CP}\ge2\sqrt{\frac{1}{\sqrt{2}}.\frac{R\sqrt{2}}{BP}.\frac{BP}{2R}}=\sqrt{2}\)

Vậy Min \(\frac{OM}{DM}+\frac{OP}{CP}=\sqrt{2}\). Dấu "=" xảy ra <=> E là điểm chính giữa cung nhỏ CD.

c) +) Chứng minh S_DPQ = S_CMN ?

Ta thấy: ^ACD = ^AEB (=45⁰) (2 góc nội tiếp chắn 2 cung bằng nhau) hay ^NEP = ^NCP

=> Tứ giác CENP nội tiếp => ^PNC = ^PEC = ^BEC = ^BDC => NP // OD (2 góc đồng vị bằng nhau)

Theo t/c diện tích miền đa giác: S_DPQ = S_NPQ + S_DPN. Do S_DPN = S_ONP (Vì NP//OD)

Nên S_DPQ = S_NOPQ (6).  Chứng minh tương tự: S_CMN = S_NMOQ   (7)

Mặt khác: Cũng từ NP // OM => S_MON = S_MOP. Tương tự: S_POQ = S_MOP => S_MON = S_POQ

Lại theo t/c diện tích miền đa giác: S_MON + S_NOQ = S_POQ + S_NOQ => S_NMOQ = S_NOPQ (8)

Từ (6),(7),(8) suy ra: S_DPQ = S_CMN (đpcm).

+) Chứng minh \(\frac{IM}{ME}+\frac{NQ}{AB}+\frac{IP}{PE}=1\)?

Dễ có các tứ giác MOCE và DOPE nội tiếp => ^MOE = ^MCE= ^DPE hay ^ICE = ^IPE => Tứ giác CEIP nội tiếp

=> ^PIE + ^PCE = ^OME + ^OCE (=180⁰) => ^PIE = ^OME

Xét \(\Delta\)EIP và \(\Delta\)EMO có: ^IPE = ^MOE (cmt); ^PIE = ^OME (cmt) => \(\Delta\)EIP ~ \(\Delta\)EMO (g.g)

=> \(\frac{IP}{PE}=\frac{MO}{OE}=\frac{MO}{OD}\). Qua ĐL Thales (MQ//OC) ta có tỉ số: \(\frac{IP}{PE}=\frac{MO}{OD}=\frac{CQ}{CD}\)

Tương tự: \(\frac{IM}{ME}=\frac{OP}{OC}=\frac{DN}{CD}\). Từ đó có:\(\frac{IM}{ME}+\frac{NQ}{AB}+\frac{IP}{PE}=\frac{DN}{CD}+\frac{NQ}{CD}+\frac{CQ}{CD}=1\)(đpcm).

Answer 2

[test o l m]

test thử cái ảnh ạ!