Cho hình chữ nhật ABCD có AB = 6; BC =4. Vẽ AHBD , gọi M là trung
điểm của HB; N là trung điểm của CD. Tính \(MA^2+MN^2\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

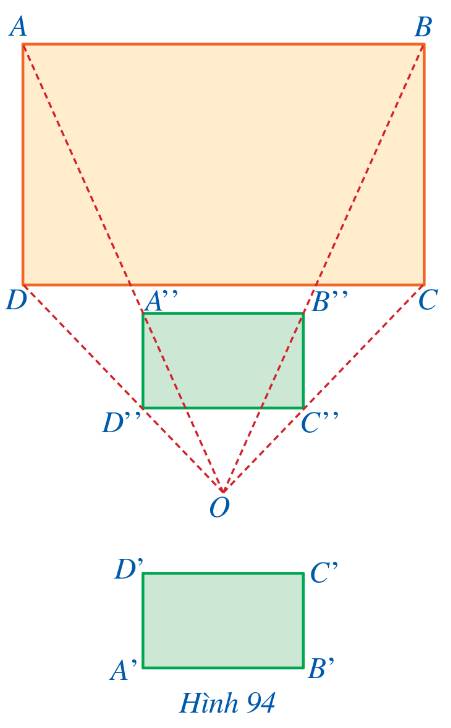
a: Xét ΔODC có D''C''//DC
nên \(\dfrac{D''C''}{DC}=\dfrac{OD''}{OD}=\dfrac{OC''}{OC}=\dfrac{3}{9}=\dfrac{1}{3}\)(1)
Xét ΔOAB có A''B"//AB
nên \(\dfrac{A"B"}{AB}=\dfrac{OA"}{OA}=\dfrac{OB"}{OB}=\dfrac{3}{9}=\dfrac{1}{3}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{OD"}{OD}=\dfrac{OC"}{OC}=\dfrac{OA"}{OA}=\dfrac{OB"}{OB}\)
mà A"A, B"B, C"C, D"D đều đi qua điểm O
nên hai hình hộp chữ nhật A"B"C"D" và ABCD đồng dạng phối cảnh với nhau
b: ta có: A'B'=C'D'=3cm
A"B"=C"D"=3cm
Do đó: A"B"=C"D"=A'B'=C'D'(3)
ta có: A'D'=B'C'=2cm
A"D"=B"C"=2cm
Do đó: A'D'=B'C'=A"D"=B"C"(4)
Từ (3),(4) suy ra hai hình hộp chữ nhật A"B"C"D" và A'B'C'D' bằng nhau

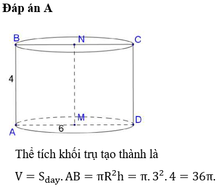
a) ABCD là Hình chữ nhật => AB = CD = 6 ( cm ) ;
Chiều dài BC = AD = 10 ( cm ).
Chu vi hình chữ nhật ABCD C = AB + BC + CD + DA = 6 + 10 + 6 + 10 = 32 ( cm )
Diện tích hcn ABCD : \(s_{ABCD}=AB.BC=6.10=60\left(cm^2\right)\)
b ) Diện tích \(\Delta ABC=\dfrac{AB.BC}{2}=\dfrac{6.10}{2}=30\left(cm^2\right)\)
a: \(C=\left(6+10\right)\cdot2=32\left(cm\right)\)
\(S=6\cdot10=60\left(cm^2\right)\)

a: BC=1/3*6=2cm
C=(6+2)*2=8*2=16cm
b: Sửa đề: Tính diện tích hình bình hành DMBN
DM=căn 3^2+3^2=3căn 2(cm)
BM=6/2=3cm
S DMBN=3*3căn 2=9*căn 2(cm2)

diện tích hình chữ nhật là : 12*24=288(cm2)
chiều cao bằng chiều rộng
chiều dài bằng đáy hình tam giác
Diện tích hình tam giác là: 288:2=144(cm2)
Đáp số : 144 cm2