Cho hình vẽ bên, biết AB = 10m; AD = 8m; AM = CN = 3m.
a) Tính diện tích hình bình hành DMBN.
b) Tính diện tích tam giác AMD và diện tích tam giác BCN. Các đại ca đại tẩu giúp đệ nhanh nhoé, thanks!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, ∠ANM = ∠CBN (=90 độ) (chúng ở vị trí đồng vị)
=> MN//BC , theo hệ quả định lý Talet ta có:
AN/AB = MN/BC, cho AB=x (cm) thì AN = x-6 (cm)
Nên: (x-6)/x=1,5/6 => x=8(cm)
Nên AB = 8 cm
b, AD là đường phân giác của tam giác ABC nên:
AB/AC = BD/DC, nếu cho BD=x (cm) thì ta có DC=5-x (cm)
Nên: 4/6=x/(5-x) => 20=10x => x=2 (cm), nên BD= 2 cm
=> DC=3 cm
Theo hình vẽ ta có: AC//BE => ∠ACD = ∠DBE (so le trong)
Xét △BDE và △CDA có:
∠ACD=∠DBE (c/m tr)
∠ADC=∠BDE (đối đỉnh)
=> △BDE=△CDA (g.g)
=> BE/AC = BD/CD => BE/6=2/3 => BE=12:3=4 (cm)
Vậy: BD= 2 cm
BE= 4 cm

Do \(DC=3EC\Rightarrow S_{ABCD}=3S_{FBCE}\)
\(\Rightarrow S_{FBCE}=\dfrac{48}{3}=16\left(m^2\right)\)


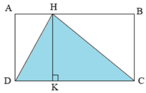
Kẻ HK vuông góc với CD, khi đó HK là chiều cao tương ứng với cạnh đáy CD.
Ta có chiều cao HK bằng chiều rộng của hình chữ nhật ABCD hay HK = BC = 24cm
Vì ABCD là hình chữ nhật nên CD = AB = 37cm.
Diện tích tam giác HDC là:
37 × 24 : 2 = 444( c m 2 )
Đáp số: 444 c m 2
Đáp án A