Cho tam giác ABC góc A = 900 ; AB=3 cm; AC=4cm
a) Tính BC, góc B, góc C
b)Phân giác của góc A cắt BC tại E. Tính BE, CE
c)Từ E kẻ EM,EN lần lượt vuông góc với AB, AC
Hỏi tứ giác AMEN là hình gì?
Tính chu vi và diện tích của tứ giác AMEN?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 4 2017
Ta có: C ^ = P ^ mà góc C và góc P là hai góc nhọn kề của tam giác ABC và tam giác MNP
Do đó để tam giác ABC và tam giác MNP bằng nhau theo trường hợp cạnh góc vuông – góc nhọn kề thì cần thêm điều kiện A C = M P
Đáp án A
23 tháng 1 2022
1: BC=10cm
Xét ΔABC có BD là đường phân giác
nên AD/AB=DC/BC
=>AD/6=DC/10
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{6}=\dfrac{CD}{10}=\dfrac{AD+CD}{6+10}=\dfrac{8}{16}=\dfrac{1}{2}\)
Do đó: AD=3(cm); BD=5(cm)
2: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{B}\) chung
Do đó: ΔABC\(\sim\)ΔHBA
Xét ΔABI và ΔCBD có
\(\widehat{ABI}=\widehat{CBD}\)
\(\widehat{IAB}=\widehat{DCB}\)
Do đó: ΔABI\(\sim\)ΔCBD
23 tháng 9 2021
a) Ta có: \(2\widehat{B}=7\widehat{C}\Rightarrow\widehat{C}=\dfrac{2}{7}\widehat{B}\)
Ta có: Tam giác ABC vuông tại A
\(\Rightarrow\widehat{B}+\widehat{C}=90^0\)
\(\Rightarrow\widehat{B}+\dfrac{2}{7}\widehat{B}=90^0\)\(\Rightarrow\dfrac{9}{7}\widehat{B}=90^0\Rightarrow\widehat{B}=70^0\)
\(\Rightarrow\widehat{C}=\dfrac{2}{7}\widehat{B}=20^0\)
b) Ta có: AD là phân giác góc A
\(\Rightarrow\widehat{DAC}=\dfrac{1}{2}\widehat{A}=45^0\)
Xét tam giác ADC có:
\(\widehat{ADC}+\widehat{DAC}+\widehat{C}=180^0\)
\(\Rightarrow\widehat{ADC}=180^0-\widehat{DAC}-\widehat{C}=180^0-45^0-20^0=115^0\)
CM
12 tháng 3 2017
S A B C = . AB. AC ≤ 1 2 . A B 2 + A C 2 2 = 1 4 . A B 2 + A C 2
Áp dụng định lý Py-ta-go cho ABC vuông tại A ta có:
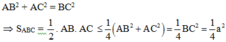
Dấu “=” xảy ra AC = AB => ∆ ABC vuông cân
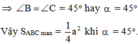
Đáp án cần chọn là: D
21 tháng 12 2021
a: Xét ΔABE và ΔDBE có
BA=BD
\(\widehat{ABE}=\widehat{DBE}\)
BE chung
Do đó: ΔABE=ΔDBE
21 tháng 4 2021
a) Xét ΔAMB và ΔAMC có
AM chung
BM=CM(M là trung điểm của BC)
AB=AC(ΔABC cân tại A)
Do đó: ΔABM=ΔACM(c-c-c)
21 tháng 4 2021
a) Ta có: ΔAMB=ΔAMC(cmt)
nên \(\widehat{BAM}=\widehat{CAM}\)(hai góc tương ứng)
mà tia AM nằm giữa hai tia AB và AC
nên AM là tia phân giác của \(\widehat{BAC}\)(đpcm)