Từ A nằm ngoài [ ở] kẻ tiếp tuyến AB, AC và cát tuyến ADE với [ ô] . Gọi H là trung điểm DE
a, CM ; tứ giác ABOC ; ABHO nội tiếp
b , CM ; AB2 = AD . AE
c , Gọi I là giao điểm của OA với BC . CM ; \(\Delta\) AID \(\wr\) \(\Delta\) AEO
d, Kẻ qua D đường thảng \(\perp\) với OB cắt BC , BE lần lượt tại K và F . CM ; DKHC nội...
Đọc tiếp
Từ A nằm ngoài [ ở] kẻ tiếp tuyến AB, AC và cát tuyến ADE với [ ô] . Gọi H là trung điểm DE
a, CM ; tứ giác ABOC ; ABHO nội tiếp
b , CM ; AB2 = AD . AE
c , Gọi I là giao điểm của OA với BC . CM ; \(\Delta\) AID \(\wr\) \(\Delta\) AEO
d, Kẻ qua D đường thảng \(\perp\) với OB cắt BC , BE lần lượt tại K và F . CM ; DKHC nội tiếp
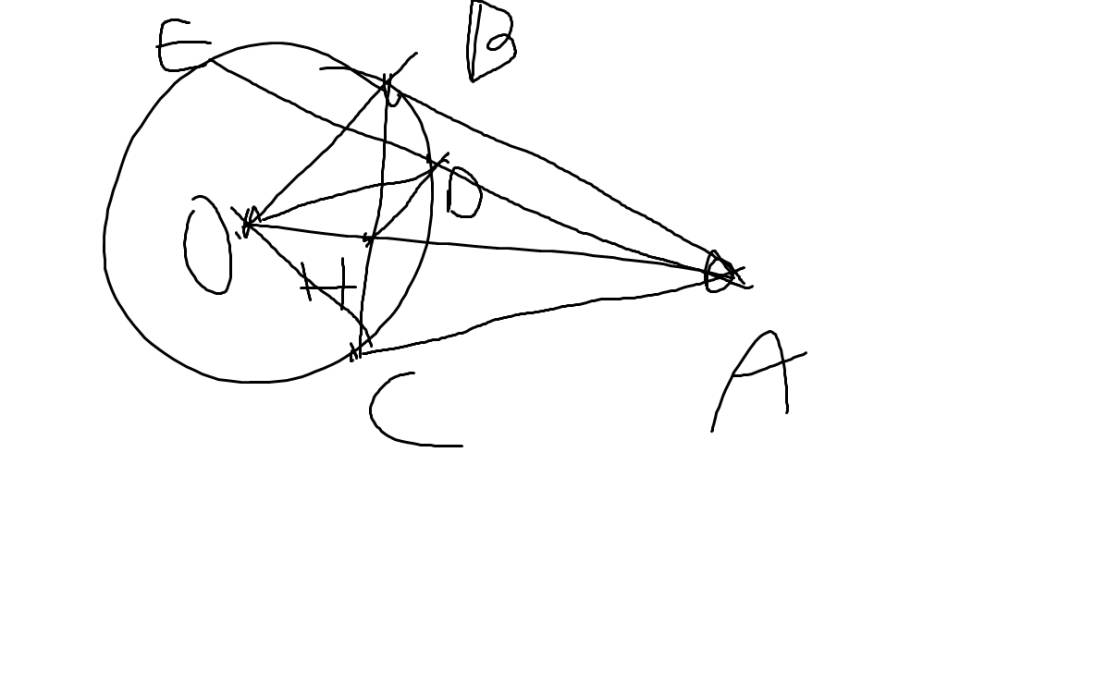
Máy mình vẽ hình không được bạn vẽ giúp mình nha
a/Tứ giác ABOC CÓ
ABO=ACO=90 độ
=>ABO+ACO=180 Độ
=>ABOC là tứ giác nội tiếp
tứ giác ABOH có
AHO=ABO=90 độ (cùng nhìn AO)
=>AHO+ABO=180 độ
=>ABOH là tứ giác nội tiếp
b/Xét ADB và ABE
A là góc chung
ABD=AEB(cùng chắn BD)
=>ADB~ABE(góc.góc)
AB/AD=AE/AB
=>AB^2=AD*AE
Hiện tại mình chỉ có thể làm đến đấy câu c và câu d mình không biết làm
uk mk cũng chưa nghĩ đc câu c , d