Cho mvà n là các số nguyên dương;
A=2+4+6+......+2m phần m
B=2+4+6+.....+2n phần n
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta thấy \(87=1.87=3.29\) nên ta xét 2TH
TH1: \(\left\{{}\begin{matrix}S\left(n\right)=1\\S\left(n+1\right)=87\end{matrix}\right.\)
Vì \(S\left(n\right)=1\) nên \(n=100...00\), do đó \(n+1=100...01\) nên \(S\left(n+1\right)=2\), mâu thuẫn.
TH2: \(\left\{{}\begin{matrix}S\left(n\right)=87\\S\left(n+1\right)=1\end{matrix}\right.\)
Vì \(S\left(n+1\right)=1\) nên \(n+1=100...00\), do đó \(n=999...99\) chia hết cho 9, dẫn đến \(S\left(n\right)⋮9\), mâu thuẫn với \(S\left(n\right)=87\)
TH3: \(\left\{{}\begin{matrix}S\left(n\right)=3\\S\left(n+1\right)=29\end{matrix}\right.\)
Vì \(S\left(n\right)=3\) nên \(n⋮3\) \(\Rightarrow n+1\) chia 3 dư 1 \(\Rightarrow S\left(n+1\right)\) chia 3 dư 1. Thế nhưng 29 chia 3 dư 2, vô lý.
TH4: \(\left\{{}\begin{matrix}S\left(n\right)=29\\S\left(n+1\right)=3\end{matrix}\right.\) . Ta lại xét các TH:
TH4.1: \(n+1=10...010...01\) hoặc \(200...01\) hoặc \(100...2\). Khi đó trong tất cả các TH thì ta đều có \(S\left(n\right)=2\), không thỏa mãn.
TH4.2: \(n+1=10...010...010...0\) hoặc \(200...0100...0\) hoặc \(100...020...0\) hoặc \(300...00\). Khi đó trong tất cả các TH thì ta đều có\(S\left(n\right)=2+9m\left(m\inℕ\right)\) với m là số chữ số 9 có trong n. Để chọn được số nhỏ nhất, ta chỉ việc lược bỏ tất cả các số 0 ở giữa và cho \(m=3\) để có \(S\left(n\right)=29\). Vậy, ta tìm được \(n=11999\) (thỏa mãn)
Vậy, số cần tìm là 11999.
Tìm các số nguyên dương n sao cho 36n-6 là tích của hai hoặc nhiều hơn các số nguyên dương liên tiếp

Đặt \(S=36^n-6\)
+Với n=1 => \(S=30=5.6\)thỏa mãn điều kiện đề bài
+Với n>1 :Ta thấy S chia hết cho 5 và 6 và không chia hết cho 4
=> \(S=5\cdot6\cdot.........\)
Do vậy để thỏa mãn đề bài thì S phải chia hết cho 7
Mà \(36^n=\left(6^n\right)^2\)chia 7 luôn dư 0,1,2,3,4
nên S không chia hết cho 7
=> với n>1 thì không có giá trị nào của n thỏa mãn đề bài
Vậy n=1 là giá trị duy nhất thỏa mãn đề bài

dễ thấy để S(n) và S(n+1) đều chia hết cho 1 số thì đuôi của n kết thúc bằng các số 9.
giả sử n có x số 9 cuối(ta tìm x nhỏ nhất)
khi đó n có dạng a 99...9 (x số 9)
=> n+1=b00...0 ( x+1 số 0) với b=a+1
do S(n) ≡ S(n+1) (mod 7) => a+9x ≡ b (mod 7) => 9x ≡ 1 (mod 7)
=> x=4
=> n=a9999
mà S(n) chia hết cho 7 => a=6 => n=69999 là nhỏ nhất thỏa mãn :D

Đáp án A
Phương pháp giải:
Để i n là số nguyên dương thì n là số nguyên dương chia hết cho 4
Lời giải:
Xét n=2k khi đó ![]() là số nguyên dương khi k chẵn.
là số nguyên dương khi k chẵn.
Kết hợp với ![]() suy ra
suy ra 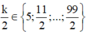 và
và ![]() là số chẵn.
là số chẵn.
Với mỗi bộ số 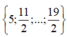 có 2 số k thỏa mãn,
có 2 số k thỏa mãn, 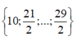 có 3 số k thỏa mãn.
có 3 số k thỏa mãn.
Vậy có tất cả 2.5+3.4=22 số thỏa mãn yêu cầu bài toán.
Sửa đề: Cho m và n là các số nguyên dương:
\(A=\dfrac{2+4+6+...+2m}{m}\)
\(B=\dfrac{2+4+6+...+2n}{n}\)
Cho A < B, so sánh m và n.
Giải:
\(A=\dfrac{\left(2+2m\right)m}{2m}=\dfrac{2\left(1+m\right)m}{2m}=1+m\)
\(B=\dfrac{\left(2+2n\right)n}{2n}=\dfrac{2\left(1+n\right)n}{2n}=1+n\)
Có \(A< B\Rightarrow1+m< 1+n\Rightarrow m< n\)