Trong không gian với hệ trục tọa độ Oxyz cho điểm . Điểm H thuộc đường thẳng sao cho đoạn MH ngắn nhất có tọa độ là:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Hình chiếu vuông góc của M(2;-1;4) lên mặt phẳng (Oxy) là điểm H(2;-1;0).

Chọn đáp án A
Hình chiếu của A x 0 ; y 0 ; z 0 lên các trục Ox, Oy, Oz lần lượt là các điểm A1 ( x 0 ;0;0), A2 (0; y 0 ;0), A3 (0;0; z 0 ).
Do đó hình chiếu của M (-2;-1;3) lên các trục Ox, Oy, Oz lần lượt là các điểm A (-2;0;0), B (0;-1;0), C (0;0;3).
Phương trình mặt phẳng theo đoạn chắn đi qua ba điểm A, B, C là: x - 2 + y - 1 + z 3 = 1

Đáp án C
Gọi E(0;0;a) theo giả thiết ta có: E M = E N ⇒ 4 + 9 + a + 2 2 = 4 + 1 + a - 4 2 ⇔ 12 a = 4 ⇔ a = 1 3 .


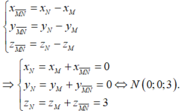



Đáp án D
Bình luận: Nhận thấy ở các đáp án chỉ có điểm
H 2 ; 3 ; 3 ∈ d .