Xác định x để 3 số 2x-1; x; 2x+1 theo thứ tự lập thành cấp số nhân
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Ba số: 2 x − 1 ; x ; 2 x + 1 theo thứ tự lập thành cấp số nhân
⇔ 2 x − 1 2 x + 1 = x 2 ⇔ 4 x 2 − 1 = x 2 ⇔ 3 x 2 = 1 ⇔ x = ± 1 3 .

Chọn B
Vì 2 x - 1 ; x ; 2 x + 1 theo thứ tự lập thành cấp số nhân nên
![]()
![]()

a.
\(D=R\)
\(f\left(-x\right)=\left|-2x-3\right|+\left|-2x+3\right|=\left|2x+3\right|+\left|2x-3\right|=f\left(x\right)\)
Hàm chẵn
b.
\(D=R\)
\(f\left(-x\right)=\dfrac{\left(-x\right)^3+\left(-x\right)}{\left(-x\right)^4+1}=\dfrac{-x^3-x}{x^4+1}=-\dfrac{x^3+x}{x^4+1}=-f\left(x\right)\)
Hàm lẻ

2) Để (d)//(1) thì \(\left\{{}\begin{matrix}2m-1=2\\-5m\ne3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2m=3\\m\ne\dfrac{-3}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{3}{2}\\m\ne-\dfrac{3}{5}\end{matrix}\right.\Leftrightarrow m=\dfrac{3}{2}\)
Vậy: Khi \(m=\dfrac{3}{2}\) thì (d)//(1)

Bài 1:
a) Để hàm số y=(k-2)x+k+3 là hàm số bậc nhất thì \(k\ne2\)
b) Để hàm số y=(k-2)x+k+3 đồng biến trên R thì k-2>0
hay k>2
Bài 2:
Thay \(x=-\dfrac{1}{2}\) và \(y=\dfrac{2}{3}\) vào (D), ta được:
\(\left(2m-3\right)\cdot\dfrac{-1}{2}-\dfrac{1}{2}=\dfrac{2}{3}\)
\(\Leftrightarrow\left(2m-3\right)\cdot\dfrac{-1}{2}=\dfrac{2}{3}+\dfrac{1}{2}=\dfrac{7}{6}\)
\(\Leftrightarrow2m-3=\dfrac{7}{6}:\dfrac{-1}{2}=\dfrac{-7}{6}\cdot\dfrac{2}{1}=-\dfrac{14}{6}=-\dfrac{7}{3}\)
\(\Leftrightarrow2m=\dfrac{-7}{3}+3=\dfrac{-7}{3}+\dfrac{9}{3}=\dfrac{2}{3}\)
hay \(m=\dfrac{1}{3}\)

Hàm xác định trên \(\left[2;3\right]\) khi và chỉ khi:
\(x^2-2x-m>0;\forall x\in\left[2;3\right]\)
\(\Rightarrow x^2-2x>m;\forall x\in\left[2;3\right]\)
\(\Rightarrow m< \min\limits_{\left[2;3\right]}\left(x^2-2x\right)\)
Xét hàm \(f\left(x\right)=x^2-2x\) trên \(\left[2;3\right]\)
\(-\dfrac{b}{2a}=1\notin\left[2;3\right]\)
\(f\left(2\right)=0\) ; \(f\left(3\right)=3\)
\(\Rightarrow\min\limits_{\left[2;3\right]}\left(x^2-2x\right)=0\)
\(\Rightarrow m< 0\)
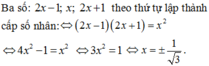
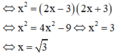

Đáp án B