Cho đường tròn (C) có đường kính là AB với A(-2; 1), B(4; 1). Khi đó phương trình của (C) là:
A. x 2 + y 2 + 2 x + 2 y + 9 = 0
B. x 2 + y 2 + 2 x + 2 y − 7 = 0
C. x 2 + y 2 - 2 x - 2 y - 7 = 0
D. x 2 + y 2 − 2 x − 2 y + 9 = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: góc AMC=1/2*180=90 độ
=>góc DMC=90 độ
góc CNB=1/2*180=90 độ
=>góc DNC=90 độ
Kẻ tiếp tuyến Cx của hai đường tròn đường kính AC,CB, Cx cắt MN tại I
Xét (E) có
IC,IM là tiếp tuyến
=>IC=IM
Xét (F) có
IN,IC là tiếp tuyến
=>IN=IC=IM
Xét ΔMCN có
CI là trung tuyến
CI=MN/2
=>ΔMCN vuông tại C
góc DMC=góc DNC=góc MCN=90 độ
=>DMCN là hcn
b: ΔDCA vuông tại C có CM vừa là đường cao
nên DM*DA=DC^2
ΔDCB vuông tại C có CN là đường cao
nên DN*DB=DC^2=DM*DA
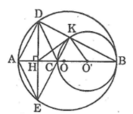
Tam giác ABD nội tiếp trong đường tròn (O) có Ab là đường kính nên vuông tại D
Suy ra: AD ⊥ BD
Tứ giác ADCE là hình thoi nên EC // AD
Suy ra: EC ⊥ BD (1)
Tam giác BCK nội tiếp trong đường tròn (O’) có BC là đường kính nên vuông tại K
Suy ra: CK ⊥ BD (2)
Từ (1) và (2) suy ra EC trùng với CK
Vậy E, C, K thẳng hàng.
Câu 1:
Gọi giao điểm của OC với AB là H
Vì OC\(\perp\)AB nên OH\(\perp\)AB tại H
=>OH là khoảng cách từ O xuống dây AB
Ta có: ΔOAB cân tại O
mà OH là đường cao
nên H là trung điểm của AB
=>HA=HB=AB/2=8(cm)
ΔOHA vuông tại H
=>\(OH^2+HA^2=OA^2\)
=>\(OH^2=10^2-8^2=36\)
=>\(OH=\sqrt{36}=6\left(cm\right)\)
Câu 2:
a: Xét (O) có
AB là đường kính
BC là dây
Do đó: AB>BC
b: Xét (O) có
ΔCAB nội tiếp
AB là đường kính
Do đó: ΔCAB vuông tại C
c: Xét ΔACB có
O là trung điểm của AB
OM//CB
Do đó: M là trung điểm của AC
Khá khó nên gạch xóa hơi nhiều
Link ảnh: https://imgur.com/a/cE1k5pV
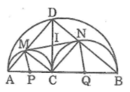
Gọi P là trung điểm của AC, Q là trung điểm của BC, I là giao điểm của MN với DC
Vì CMDN là hình chữ nhật nên IC = IM = ID = IN
Tam giác CNI cân tại I nên 
(3)
Tam giác CNQ cân tại Q nên 
(4)
Vì AB ⊥ CD nên 
=
90
°
(5)
Từ (3), (4) và (5) suy ra: 
=
90
°
hay MN ⊥ QN
Vậy MN là tiếp tuyến của đường tròn đường kính BC
Tam giác CMI cân tại I nên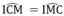 
(6)
Tam giác CMP cân tại P nên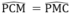 
(7)
Vì AB ⊥ CD nên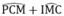 
=
90
°
(8)
Từ (6), (7) và (8) suy ra: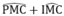 
=
90
°
hay MN ⊥ PM
Vậy MN là tiếp tuyến của đường tròn đường kính AC
Tọa độ trung điểm I của AB là: x = − 2 + 4 2 = 1 y = 1 + 1 2 = 1
Đường tròn có tâm I(1; 1) là trung điểm của AB và có bán kính R = I A = ( − 2 − 1 ) 2 + ( 1 − 1 ) 2 = 3 nên phương trình của đường tròn là:
x − 1 2 + y − 1 2 = 9 ⇔ x 2 + y 2 − 2 x − 2 y − 7 = 0
ĐÁP ÁN C