Với vị trí nào của m thì 2 đường thẳng sau đây vuông góc
△1: (2m-1)x+my-10=0; △2: \(\left\{{}\begin{matrix}x=2-3t\\y=1-4mt\end{matrix}\right.\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 8 2017
Đường thẳng Δ1 có vectơ pháp tuyến là 
.
Đường thẳng Δ2 có vectơ pháp tuyến là 
.
Hai đường thẳng vuông góc khi và chỉ khi 
Suy ra : m( m-1) + m+ 1= 0 hay m2+1 = 0 phương trình vô nghiệm.
Vậy không có giá trị của m để hai đường thẳng vuông góc.
Chọn C.
CM
20 tháng 7 2017
+ đường thẳng ∆1 có VTCP
+ đường thẳng ∆2 có VTCP
Để hai đường thẳng vuông góc thì
Nên: -3( m2+ 1) +(-m) .(-4m) = 0 =>m2-3= 0=>
Chọn A.
HQ
Hà Quang Minh
Giáo viên
29 tháng 9 2023
Vecto pháp tuyến của là: \(\overrightarrow {{n_1}} = \left( {m; - 1} \right)\)
Vecto pháp tuyến của là: \(\overrightarrow {{n_2}} = \left( {2; - 1} \right)\)
Vậy ai đường thẳng \({\Delta _1}\),\({\Delta _2}\) vuông góc với nhau khi và chỉ khỉ \(\overrightarrow {{n_1}} ;\overrightarrow {{n_2}} \) vuông góc với nhau tức là \(\overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 0 \Leftrightarrow 2m + 1 = 0 \Leftrightarrow m = \frac{{ - 1}}{2}\)
CM
14 tháng 9 2019
+ Hai đường thẳng cắt nhau tại một điểm trên trục hoành suy ra tung độ giao điểm là y=0.
+ Từ đây ta có: (m-1)x-5=9 suy ra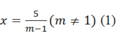 
Đồng thời: mx+7=0 suy ra x= -7/m ( m≠0) (2)
+ Từ (1) và (2) ta có: 
Chọn D.
15 tháng 11 2021
Ghi lại đề: \(y=\left(m+1\right)x-3;y=\left(2m-1\right)x+4\)
\(a,m=-\dfrac{1}{2}\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{1}{2}x-3\\y=-2x+4\end{matrix}\right.\)
Hệ số a 2 đt đã cho là \(\dfrac{1}{2};-2\) có tích là -1 nên 2 đt vuông góc
\(b,\Leftrightarrow\left(m+1\right)\left(2m-1\right)=-1\\ \Leftrightarrow2m^2+m-1=-1\\ \Leftrightarrow2m^2+m=0\\ \Leftrightarrow m\left(2m-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=0\\m=\dfrac{1}{2}\end{matrix}\right.\)
\(\Delta_1\) nhận \(\left(2m-1;m\right)\) là 1 vtpt
\(\Delta_2\) nhận \(\left(-3;-4m\right)\) là 1 vtcp \(\Rightarrow\) nhận \(\left(4m;-3\right)\) là 1 vtpt
Để 2 đường thẳng vuông góc
\(\Leftrightarrow2m.4m+m.\left(-3\right)=0\Leftrightarrow8m^2-3m=0\Rightarrow\left[{}\begin{matrix}m=0\\m=\frac{3}{8}\end{matrix}\right.\)