Tính \(A=23x-9y\) biết x,y > 0; \(x^2+y^2+\frac{1}{x^2}+\frac{1}{y^2}=4\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
16 tháng 3 2018
Ta có 2 3 x − 9 y + 6 x + y = 3 4 x − 3 y − 9 x + y = 1 ⇔ 2 3 . 1 x − 3 y + 6. 1 x + y = 3 4. 1 x − 3 y − 9. 1 x + y = 1
Đặt 1 x − 3 y = a ; 1 x + y = b ta được hệ phương trình 2 3 a + 6 b = 3 4 a − 9 b = 1
Đáp án: D
31 tháng 1 2021
có nhiều cách vd
x+y=4 và |2x+1|+|y-x|=5
vì x+y=4 =>x=4-y => |2(4-y)+1|+|y-(4-y)|=5 => |9-2y|+|2y-4|=5; Dâú "="xảy ra khi: |9-2y|+|2y-4| >=|9-2y+2y-4|=5 => (9-2y)(2y-4)>=0
=>9-2y>=0 và 2y-4>=0 hoặc 9-2y<=0 và 2y-4<=0
đến dây bn tự hiểu nhé
NQ
4
TN
20 tháng 2 2016
23x +53y=109
<=> x = (109 - 53y)/23 = 4 - 2y +(17-7y)/23
x nguyên nên 17-7y= 23m => y = (17-23m)/7 = 2 -3m +(3 - 2m)/7
y nguyên nên: 3 - 2m = 7n => m = (3-7n)/2 = 1 - 3n +(1 -n)/2
m nguyên nên: 1 -n = 2p => n = 1-2p
(m,n,p là số nguyên)
Từ n = 1-2p => m = 1 - 3(1-2p) + p = -2 +7p
=> y = 2 -3(-2+7p) + 1- 2p = 9 -23p
=> x = 4 - 2(9 -23p) -2 +7p = 2 -18 +46p +7p = 53p - 16.
Vậy x = 53p - 16; y = 9 - 23p
LD
4
3 tháng 4 2017
xin lỗi mk mới lớp 7 nhưng bn hãy vận dụng ng~ j bn đã học bn sẽ làm được..
-----chúc bn học tốt-------
15 tháng 11 2018
\(3x^2+2y^2=7xy\)
\(\Leftrightarrow3x^2-7xy+2y^2=0\)
\(\Leftrightarrow3x^2-6xy-xy+2y^2=0\)
\(\Leftrightarrow3x\left(x-2y\right)-y\left(x-2y\right)=0\)
\(\Leftrightarrow\left(3x-y\right)\left(x-2y\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-y=0\\x-2y=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}3x=y\\x=2y\end{matrix}\right.\)
+) TH1 : \(y=3x\)
\(\Leftrightarrow A=\dfrac{3x+y}{7y-x}+\dfrac{6x-9y}{2x+y}\)
\(=\dfrac{3x+3x}{7.3x-x}+\dfrac{6x-9.3x}{2x+3x}\)
\(=\dfrac{9x}{20x}+\dfrac{-21x}{5x}\)
\(=-\dfrac{15}{4}\)
+) TH2 : \(x=2y\)
\(\Leftrightarrow A=\dfrac{3x+y}{7y-x}+\dfrac{6x-9y}{2x+y}\)
\(=\dfrac{3.2y+y}{7y-2y}+\dfrac{6.2y-9y}{2.2y+y}\)
\(=\dfrac{7y}{5y}+\dfrac{3y}{5y}\)
\(=2\)
Vậy...
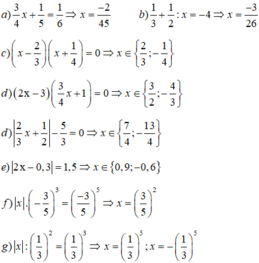
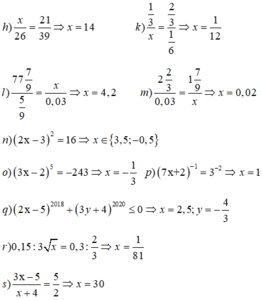
Ta có :
\(x^2+y^2+\frac{1}{x^2}+\frac{1}{y^2}=4\)
\(\Leftrightarrow\left(x^2+\frac{1}{x^2}-2\right)+\left(x^2+\frac{1}{y^2}-2\right)=0\)
\(\Leftrightarrow\left(x-\frac{1}{x}\right)^2+\left(y-\frac{1}{y}\right)^2=0\)
Lại có :
\(\left\{{}\begin{matrix}\left(x-\frac{1}{x}\right)^2\ge0\\\left(y-\frac{1}{y}\right)^2\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left(x-\frac{1}{x}\right)^2+\left(y-\frac{1}{y}\right)^2\ge0\)
Dấu "=" xảy ra : \(\Leftrightarrow\left\{{}\begin{matrix}x-\frac{1}{x}=0\\y-\frac{1}{y}=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
Khi đó :
\(A=23.1-9.1=14\)
Vậy...