Tìm x nguyên để các biểu thức sau nhận giá trị nguyên :
\(A=\frac{1-2\text{x}}{x+3}\) ; \(B=\frac{2012\sqrt{x}+5}{1006\sqrt{x}+1}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 4 2018
\(a)\) Ta có :
\(A=\frac{6x+9}{3x+2}=\frac{6x+4+5}{3x+2}=\frac{6x+4}{3x+2}+\frac{5}{3x+2}=\frac{2\left(3x+2\right)}{3x+2}+\frac{5}{3x+2}=2+\frac{5}{3x+2}\)
Để A có giá trị nguyên thì \(\frac{5}{3x+2}\) phải nguyên hay \(5\) chia hết cho \(3x+2\)\(\Rightarrow\)\(\left(3x+2\right)\inƯ\left(5\right)\)
Mà \(Ư\left(5\right)=\left\{1;-1;5;-5\right\}\)
Suy ra :
| \(3x+2\) | \(1\) | \(-1\) | \(5\) | \(-5\) |
| \(x\) | \(\frac{-1}{3}\) | \(-1\) | \(1\) | \(\frac{-7}{3}\) |
Mà \(x\) là số nguyên nên \(x\in\left\{-1;1\right\}\)
Vậy \(x\in\left\{-1;1\right\}\)
Chúc bạn học tốt ~
19 tháng 4 2018
\(b)\) Ta có bất đẳng thức giá trị tuyệt đối như sau :
\(\left|x\right|+\left|y\right|\ge\left|x+y\right|\)
Dấu "=" xảy ra khi và chỉ khi \(xy\ge0\)
Áp dụng vào ta có :
\(A=\left|x\right|+\left|8-x\right|\ge\left|x+8-x\right|=\left|8\right|=8\)
Dấu "=" xảy ra khi và chỉ khi \(x\left(8-x\right)\ge0\)
Trường hợp 1 :
\(\hept{\begin{cases}x\ge0\\8-x\ge0\end{cases}\Leftrightarrow\hept{\begin{cases}x\ge0\\x\le8\end{cases}\Leftrightarrow}0\le x\le8}\)
Trường hợp 2 :
\(\hept{\begin{cases}x\le0\\8-x\le0\end{cases}\Leftrightarrow\hept{\begin{cases}x\le0\\x\ge8\end{cases}}}\) ( loại )
Vậy GTNN của \(A=8\) khi \(0\le x\le8\)
Chúc bạn học tốt ~
11 tháng 6 2021
a) C được xác định <=> x khác +- 2
b) Ta có : \(C=\dfrac{x^3}{\left(x-2\right)\left(x+2\right)}-\dfrac{x\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}-\dfrac{2\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^3-x^2-2x-2x+4}{\left(x-2\right)\left(x+2\right)}=\dfrac{x^2\left(x-1\right)-4\left(x-1\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{\left(x-1\right)\left(x-2\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=x-1\)
Để C = 0 thì x - 1 = 0 <=> x = 1 (tm)
c) Để C nhận giá trị dương thì x - 1 > 0 <=> x > 1
Kết hợp với ĐK => Với x > 1 và x khác 2 thì C nhận giá trị dương
PK
15 tháng 1 2023
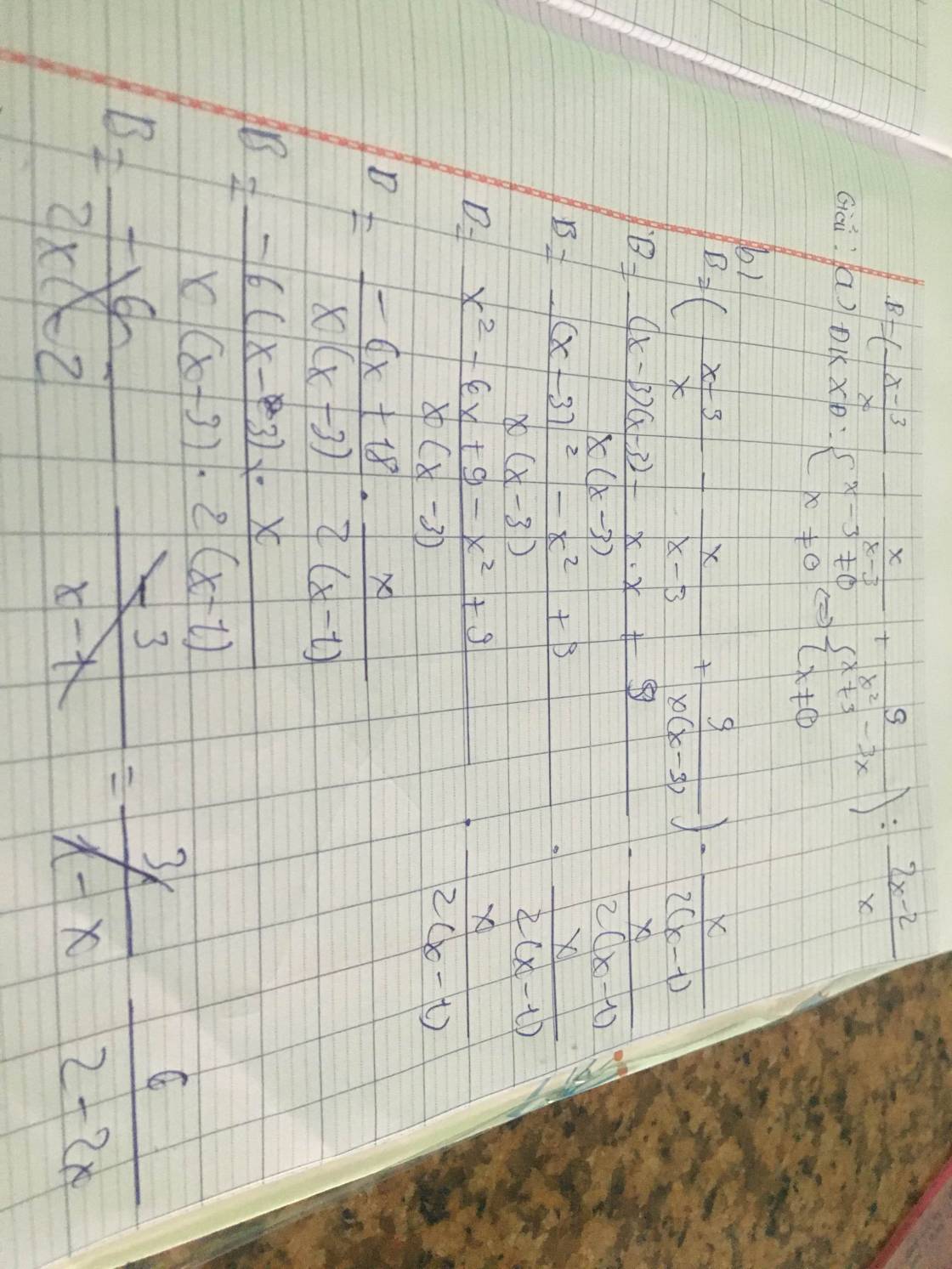c/
Ta có : B=2=>6/2-2x
<=>6=4-4x
<=>6-4=-4x
<=>-4x=2
<=>x=2/-4=-1/2
d/ĐKXĐ:2-2x≠0
<=>2(1-x)≠0<=>-2(x-1)≠0
<=>x≠1
Để giá trị của biểu thức B nguyên thì 2-2x là Ư(6)
=>2-2x ∈ Ư(6)={±1;±2;±3;±6) Nếu 2-2x=1=> -2x=-1=>x=1/2( thoả mãng)
Rồi còn nhiêu bạn tự xét trường hợp y trang cách làm ở trênn nnhan :;)).À sẽ có mấy cái trường hợp nó giống ĐKXĐ thì bạn ghi trong ngoặc ko thoã mãn nhan.
28 tháng 3 2017
đế phân số nhận giá trị nguyên
=>10x+15 chia hết cho 5x+1
=>10x+2+13 chia hết cho 5x+1
=>2(5x+1)+13 chia hết cho 5x+1
vì 5x+1 chia hết cho 5x+1
=>2(5x+1) chia hết cho 5x+1
=>13 chia hết cho 5x+1
=>5x+1 thuộc Ư(13)={1;13;-1;-13}
=>5x+1 thuộc {1;13;-1;-13}
=>5x thuộc {0;12;-2;-14}
=>x thuộc {0;2,4;-0,4;-2,8}
vì x có các giá trị nguyên
=>x=0
vậy x=0
LH
0
10 tháng 12 2020
Để P nguyên thì 2x-1⋮2x+1
⇔2x+1-2⋮2x+1
mà 2x+1⋮2x+1
nên -2⋮2x+1
⇔2x+1∈Ư(-2)
⇔2x+1∈{1;-1;2;-2}
⇔2x∈{0;-2;1;-3}
⇔\(x\in\left\{0;-1;\dfrac{1}{2};-\dfrac{3}{2}\right\}\)
mà x nguyên
nên x∈{0;-1}
Vậy: x∈{0;-1}