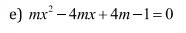giải pt ; [ x2 - 4x +2 ]2 +x2 - 4x - 4 = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2:
a: y1+y2=-(x1+x2)=-5
y1*y2=(-x1)(-x2)=x1x2=6
Phương trình cần tìm có dạng là;
x^2+5x+6=0
b: y1+y2=1/x1+1/x2=(x1+x2)/x1x2=5/6
y1*y2=1/x1*1/x2=1/x1x2=1/6
Phương trình cần tìm là:
a^2-5/6a+1/6=0


`x^2 + 2(m-1)x + m^2 = 0`
Thay `m=0` vào pt và giải ta được :
`x^2 - 6x + 16 = 0`
Vì `x^2 - 6x + 16 > 0` với mọi `x`
`=>` vô nghiệm
Vậy `S = RR`
Thay `m=-4` vào pt và giải ta được :
`x^2 + 10x + 16 = 0`
`\Delta = 10^2 - 4*1*16 = 36 > 0`
`=> \sqrt{\Delta} = 6`
`=>` Phương trình có 2 nghiệm phân biệt :
`x_1 = (-10+6)/(2*1) = -2`
`x_2 = (-10-6)/(2*1) = -8`
Vậy `S = {-2,-8}`

\(\text{∆}=\left(-4m\right)^2-4.m.\left(4m-1\right)\)
\(=16m^2-16m^2+4m\)
\(=4m\)
phương trình vô nghiệm khi \(\text{∆}< 0\)
\(\Rightarrow4m< 0\)
⇒ \(m< 0\)
`\Delta'=(-2m)^2-m(4m-1)=4m^2-4m^2+m=m`
Để phương trình vô nghiệm thì `\Delta'<0 => m<0`

a.Bạn thế vào nhé
b.\(\Delta=3^2-4m=9-4m\)
Để pt vô nghiệm thì \(\Delta< 0\)
\(\Leftrightarrow9-4m< 0\Leftrightarrow m>\dfrac{9}{4}\)
c.Ta có: \(x_1=-1\)
\(\Rightarrow x_2=-\dfrac{c}{a}=-m\)
d.Theo hệ thức Vi-ét, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-3\\x_1.x_2=m\end{matrix}\right.\)
1/ \(x_1^2+x_2^2=34\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=34\)
\(\Leftrightarrow\left(-3\right)^2-2m=34\)
\(\Leftrightarrow m=-12,5\)
..... ( Các bài kia tương tự bạn nhé )

\(\Delta=\left(2m-1\right)^2-8\left(m-1\right)=4m^2-12m+9=\left(2m-3\right)^2\ge0\) ; \(\forall m\)
\(\Rightarrow\) Phương trình đã cho luôn có 2 nghiệm với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-2m+1}{2}\\x_1x_2=\dfrac{m-1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2\left(x_1+x_2\right)=-2m+1\\4x_1x_2=2m-2\end{matrix}\right.\)
Cộng vế với vế:
\(\Rightarrow2\left(x_1+x_2\right)+4x_1x_2=-1\)
Đây là hệ thức liên hệ các nghiệm ko phụ thuộc m

a)Thay m=-2 vào biểu thức ta có:
\(\left(2.-2\right)\left(x+3\right)=-\left(-2\right)x+5\)
\(\Leftrightarrow-4\left(x+3\right)=4x+5\)
\(\Leftrightarrow-4x-12=4x+5\)
\(\Leftrightarrow-4x-4x=12+5\)
\(\Leftrightarrow-8x=17\)
\(\Leftrightarrow x=\dfrac{-17}{8}\)
Nếu m=-2 thì \(x=\dfrac{-17}{8}\)
còn m=\(\dfrac{1}{2}\) thì bạn làm tương tự
mấy câu kia lát mình làm sau giờ mình bận rồi
a/ +) Với m = -2 ta có:
\(\left(2\cdot\left(-2\right)-1\right)\left(x+3\right)=-\left(-2x\right)+5\)
\(\Leftrightarrow-5\left(x+3\right)=2x+5\Leftrightarrow-5x-2x=5+15\)
\(\Leftrightarrow-7x=20\Leftrightarrow x=-\dfrac{20}{7}\)
Vậy khi m = -2 thì x = -20/7
+) Với m = 1/2 ta có:
\(\left(2\cdot\dfrac{1}{2}-1\right)\left(x+3\right)=-\dfrac{1}{2}x+5\)
\(\Leftrightarrow\dfrac{1}{2}x=5\Leftrightarrow x=10\)
Vậy khi m = 1/2 thì x = 10
b/ pt có nghiệm = -2
=> \(2m-1=2m+5\Leftrightarrow0\cdot m=6\left(voli\right)\)
Vậy không có gt của m nào t/m để pt có nghiệm x = -2
c/ (2m-1)(x+3) = -mx + 5
\(\Leftrightarrow2mx+6m-x+mx-3=5\)
\(\Leftrightarrow3mx-x=5-6m+3\)
\(\Leftrightarrow x\left(3m-1\right)=-6m+8\Leftrightarrow x=\dfrac{-6m+8}{3m-1}\)

a) Thay m=1 vào phương trình, ta được:
\(x^2-2\cdot\left(1+2\right)x+8=0\)
\(\Leftrightarrow x^2-6x+8=0\)
\(\Leftrightarrow x^2-4x-2x+8=0\)
\(\Leftrightarrow x\left(x-4\right)-2\left(x-4\right)=0\)
\(\Leftrightarrow\left(x-4\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-4=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=2\end{matrix}\right.\)
Vậy: Khi m=1 thì phương trình có hai nghiệm phân biệt là \(x_1=4;x_2=2\)
ad cho em hỏi em giải theo cách của anh thì ra đúng nghiệm mà sao lập delta với delta đều ra 2 với -4 anh. sao ý anh giúp em với. với lại ý em thấy đề câu b cũng sai nữa ạ

\(1-sin^23x-5sin3x+5=0\)
\(\Leftrightarrow-sin^23x-5sin3x+6=0\)
\(\Rightarrow\left[{}\begin{matrix}sin3x=1\\sin3x=-6< -1\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow3x=\dfrac{\pi}{2}+k2\pi\)
\(\Rightarrow x=\dfrac{\pi}{6}+\dfrac{k2\pi}{3}\)

\(\Leftrightarrow1-sin^22x+3sin2x-3=0\)
\(\Leftrightarrow-sin^22x+3sinx-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=1\\sin2x=2>1\left(ktm\right)\end{matrix}\right.\)
\(\Rightarrow2x=\dfrac{\pi}{2}+k2\pi\)
\(\Rightarrow x=\dfrac{\pi}{4}+k\pi\)