Câu 1. Cho tam giác ABC vuông tại A (AB<AC). Tia phân giác góc A cắt BC tại D. Trên cạnh AC lấy điểm M sao cho AM=ABa) Chứng minh: DB=DMb) Gọi E là giao điểm AB và MD. Chứng minh \(\Delta BED=\Delta MCD\)c) Gọi H là trung điểm của EC. Chứng minh ba điểm A,D,H thẳng hàngCâu 2 . Cho \(\Delta ABC\)có AB<AC. Tia phân giác góc ABC cắt AC tại D. Trên cạnh BC lấy điểm E sao cho BA=BEa) Chứng minh: DA=DEb) Tia ED cắt BA tại F....
Đọc tiếp
Câu 1. Cho tam giác ABC vuông tại A (AB<AC). Tia phân giác góc A cắt BC tại D. Trên cạnh AC lấy điểm M sao cho AM=AB
a) Chứng minh: DB=DM
b) Gọi E là giao điểm AB và MD. Chứng minh \(\Delta BED=\Delta MCD\)
c) Gọi H là trung điểm của EC. Chứng minh ba điểm A,D,H thẳng hàng
Câu 2 . Cho \(\Delta ABC\)có AB<AC. Tia phân giác góc ABC cắt AC tại D. Trên cạnh BC lấy điểm E sao cho BA=BE
a) Chứng minh: DA=DE
b) Tia ED cắt BA tại F. Chứng minh \(\Delta DAF=\Delta DEC\)
c) Gọi H là trung diểm của FC. Chứng minh ba điểm B,D,H thẳng hàng
Câu 3. Cho \(\Delta ABC\)cân tại A. Kẻ AH vuông góc với BC (\(H\in BC\))
a) Chứng minh: HB=HC
b) Kẻ \(HD\perp AB\left(D\in AB\right)\)và \(HE\perp AC\left(E\in AC\right)\). Chứng minh \(\Delta HDE\)cân
Câu 4. Cho tam giác ABC vuông tại B, đường phân giác \(AD\left(D\in BC\right)\). Kẻ DE vuông góc với \(AC\left(E\in AC\right)\)
a) Chứng minh: \(\Delta ABD=\Delta AED;\)
b) BE là đường trung trực của đoạn thẳng AD
c) Gọi F là giao điểm của hai đường thẳng AB và ED Chứng minh BF=EC

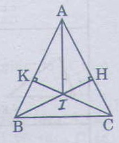
a) Chứng minh ΔBHC=ΔCKB
Xét ΔBHC vuông tại H và ΔCKB vuông tại K có
BC là cạnh chung
\(\widehat{HCB}=\widehat{KBC}\)(\(\widehat{ACB}=\widehat{ABC}\), H∈AC, K∈AB)
Do đó: ΔBHC=ΔCKB(cạnh huyền-góc nhọn)
b)
*Chứng minh IB=IC
Ta có: ΔBHC=ΔCKB(cmt)
⇒\(\widehat{HBC}=\widehat{KCB}\)(hai góc tương ứng)
hay \(\widehat{IBC}=\widehat{ICB}\)
Xét ΔIBC có \(\widehat{IBC}=\widehat{ICB}\)(cmt)
nên ΔIBC cân tại I(định lí đảo của tam giác cân)
⇒IB=IC(đpcm)
*Chứng minh \(\widehat{IBK}=\widehat{ICH}\)
Ta có: \(\widehat{ABH}+\widehat{HBC}=\widehat{ABC}\)(tia BH nằm giữa hai tia BA,BC)
\(\widehat{ACK}+\widehat{BCK}=\widehat{ACB}\)(tia CK nằm giữa hai tia CA,CB)
mà \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy của ΔABC cân tại A)
và \(\widehat{HBC}=\widehat{KCB}\)(cmt)
nên \(\widehat{ABH}=\widehat{ACK}\)
hay \(\widehat{IBK}=\widehat{ICH}\)(đpcm)
c) Chứng minh KH//BC
Ta có: ΔBKC=ΔBHC(cmt)
⇒KB=HC(hai cạnh tương ứng)
Ta có: AK+KB=AB(A,K,B thẳng hàng)
AH+HC=AC(do A,H,C thẳng hàng)
mà AB=AC(ΔABC cân tại A)
và KB=HC(cmt)
nên AK=AH
Xét ΔAKH có AK=AH(cmt)
nên ΔAKH cân tại A(định nghĩa tam giác cân)
⇒\(\widehat{AKH}=\frac{180^0-\widehat{A}}{2}\)(số đo của một góc ở đáy trong ΔAKH cân tại A)(1)
Ta có: ΔABC cân tại A(gt)
⇒\(\widehat{ABC}=\frac{180^0-\widehat{A}}{2}\)(số đo của một góc ở đáy trong ΔABC cân tại A)(2)
Từ (1) và (2) suy ra \(\widehat{AKH}=\widehat{ABC}\)
mà \(\widehat{AKH}\) và \(\widehat{ABC}\) là hai góc ở vị trí đồng vị
nên KH//BC(dấu hiệu nhận biết hai đường thẳng song song)
A B C H K I a.Do △ABC cân ⇒∠ABC=∠ACB
Xét △BHC= △CKB (cạnh huyền-góc nhọn)
⇒∠IBC=∠ICB (2 góc tương ứng)
b. Do ∠IBC =∠ICB (câu a)
⇒△IBC cân ⇒ IB=IC
Xét △IBK=△ICH (cạnh huyền-góc nhọn)
⇒∠IBK=∠ICH (2 góc tương ứng)
c. Do △BHC=△CKB (câu a)
⇒ BH=CK (2 cạnh tương ứng)
⇒HC=KB ( 2 cạnh tương ứng)
Xét △BHK=△CKH(c.c.c)
⇒ ∠BHK=∠CKH (2 góc tương ứng)
Xét △IKH có: ∠2IHK=1800 -∠ KIH
Xét △IBC có : ∠2IBC=1800 -∠ ICB -∠BIC
Mà ∠BIC=∠KIH (2góc đối đỉnh)
⇒∠2IBC=1800-∠KIH
⇒∠IBC=∠IHK
Mà ∠IBC và ∠IHK là 2 góc so le trong
⇒KH // BC
Còn câu d thì hình như bị thiếu dữ kiện nên mik chưa làm
Chúc bn hok tốt