chứng minh công thức;
\(1^2+2^2+3^2+......+n^2=n\left(n+1\right)\left(2n+1\right)\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chứng minh Udây = √3Upha
Ta có: Udây = U13 = U12 = U23; Upha = UO1 = UO2 = UO3 là các giá trị hiệu dụng của hiệu điện thế pha.
Dùng giản đồ vectơ
Hiệu điện thế dây từ A2 đến A1 là: u12 = u1O + uO2 = u1O – u2O → U1O→ - U2O→ = U12→
Vì u2O, u1O là 2 nguồn xoay chiều cùng biên độ và lệch pha nhau 2π/3
Theo quy tắc cộng vecto (hình bình hành)
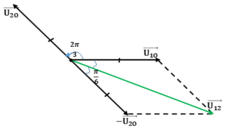
Ta có: U12 = 2U1O.cos(π/6) = U1O.√3
Vậy Ud = √3Up




- Nếu k là một hằng số thì (ku)’ = ku’
Thật vậy, ta có: (ku)' = k'u + ku' = 0.u + ku' = ku'
Do đạo hàm của hàm hằng bằng 0
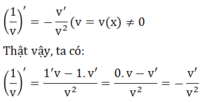

Ta có: \(\text{℘}=\dfrac{A}{t}\)
\(\Rightarrow\text{℘}=\dfrac{F.s}{t}\)
\(\Rightarrow\text{℘}=F.\dfrac{s}{t}\)
\(\Rightarrow\text{℘}=F.v\)

Ta có công thức tính áp suất là p = F/S.
Trọng lực P = mg của khối chất lỏng chính là lực F tác dụng lên diện tích đáy S của khối chất lỏng.
=> p = F/S = P/S = mg/S
Mà ta có trọng lượng riêng của chất lỏng là: d = mg/V => mg = d/V
mà V = S.h => mg = d/Sh
=> p = mg/S = (d/Sh) / S = d.h
Vậy p=d.h
Bài làm
Ta có công thức tính áp suất là p = F/S.
Trọng lực P = mg của khối chất lỏng chính là lực F tác dụng lên diện tích đáy S của khối chất lỏng.
=> p = F/S = P/S = mg/S
Mà ta có trọng lượng riêng của chất lỏng là: d = mg/V => mg = d/V
mà V = S.h => mg = d/Sh
=> p = mg/S = (d/Sh) / S = d.h
Vậy p = d . h
# Học tốt #
12 +22+32+...+n2
= 1.(2-1)+2.(3-1)+3.(4-1)+...+n.(n+1-1)
= (1.2+2.3+3.4+...+n.n(n+1)) - (1+2+3+...+n)
Dat A = 1.2+2.3+3.4+...+n.(n+1)
=> 3A = 1.2.3+2.3.3+3.4.3+...+n.(n+1).3
3A = 1.2.3+2.3(4-1)+3.4.(5-2)+...+n.(n+1).(n+2-n+1)
3A = (1.2.3+2.3.4+3.4.5+...+n.(n+1).(n+2)) - (1.2.3+2.3.4+...+(n-1).n.(n+1))
3A = n.(n+1).(n+2)
\(\Rightarrow A=\frac{n.\left(n+1\right).\left(n+2\right)}{3}\)
ta co: 1+2+...+n = n.(n+1)/2
=> \(1^2+2^2+...+n^2=\frac{n.\left(n+1\right).\left(n+2\right)}{3}-\frac{n.\left(n+1\right)}{2}=\frac{n.\left(n+1\right).\left(2n+1\right)}{6}\)
cop sai de hay sao z bn???
Sửa đề : 12 + 22 + 32 + ... + n2 = \(\frac{n\left(n+1\right)\left(2n+1\right)}{6}\)
VT <=> 1 ( 2 - 1 ) + 2 ( 3 - 1 ) + 3 ( 4 - 1 ) + ... + n [ ( n + 1 ) - 1 ]
= [ 1 . 2 + 2 . 3 + 3 . 4 + ... + n ( n + 1 ) ] - ( 1 + 2 + 3 + 4 + ... + n )
Đặt A = 1 . 2 + 2 . 3 + 3 . 4 + ... + n ( n + 1 ) . Ta có :
3A = 1.2.3 + 2.3.3 + 3.4.3 + ... + 3n ( n + 1 )
=> 3A = 1.2.3 + 2.3 ( 4 - 1 ) + 3.4 ( 5 - 2 ) + ... + n ( n + 1 ) [ ( n + 2 ) - ( n - 1 ) ]
=> 3A = 1.2.3 + 2.3.4 - 1.2.3 + 3.4.5 - 2.3.4 + ... + n ( n + 1 ) ( n + 2 ) - ( n - 1 ) n ( n + 1 )
=> 3A = n ( n + 1 ) ( n + 2 )
=> A = \(\frac{n\left(n+1\right)\left(n+2\right)}{3}\)
=> VT = \(\frac{n\left(n+1\right)\left(n+2\right)}{3}\)- ( 1 + 2 + 3 + 4 + ... + n )
= \(\frac{n\left(n+1\right)\left(n+2\right)}{3}-\frac{\left(n+1\right)n}{2}\)
\(=\frac{2n\left(n+1\right)\left(n+2\right)-3n\left(n+1\right)}{6}\)
\(=\frac{n\left(n+1\right)\left(n+2\right)}{6}=VP\)( Đpcm )