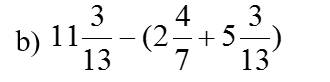
a: Số đoạn thẳng tạo thành là:

\(\dfrac{26\left(26-1\right)}{2}=13\cdot25=325\left(đoạn\right)\)

b: Theo đề, ta có: \(C^2_n=496\)

=>\(\dfrac{n!}{\left(n-2\right)!\cdot2!}=496\)

=>n(n-1)=496*2=992

=>\(n^2-n-992=0\)

=>\(\left[{}\begin{matrix}n=32\left(nhận\right)\\n=-31\left(loại\right)\end{matrix}\right.\)

c: Số điểm còn lại là 26-4=22(điểm)

TH1: Lấy 1 điểm trong 4 điểm thẳng hàng, lấy 1 điểm trong 22 điểm còn lại

=>Có 4*22=88(đường)

TH2: vẽ 1 đường thẳng đi qua 4 điểm thẳng hàng

=>Có 1 đuờng

TH3: Lấy 2 điểm trong 22 điểm còn lại

=>Có \(C^2_{22}=231\left(đường\right)\)

Số đường thẳng là: 231+1+88=320 đường

Lời giải:

1. Ba điểm thẳng hàng là $K,M,A$ và điểm $M$ nằm giữa $K,A$

2. Hai tia đối nhau: $MK, MA$

Khoảng năm 776, Phùng Hưng cùng em là Phùng Hải đã họp quân khởi nghĩa ở Đường Lâm. Nhân dân các vùng xung quanh nổi dậy hưởng ứng và giành được quyền làm chủ vùng đất của mình.

ít lâu sau, Phùng Hưng kéo quân về bao vây phủ thành Tống Bình. Viên đô lộ là Cao Chính Bình phải rút vào thành cố thủ, rồi sinh bệnh chết. Phùng Hưng chiếm được thành, sắp đặt việc cai trị.

Phùng Hưng mất, con trai là Phùng An nối nghiệp cha. Năm 791, nhà Đường đem đại quân sang đàn áp, Phùng An ra hàng.

- Khoảng năm 776, Phùng Hưng cùng em là Phùng Hải đã họp quân khởi nghĩa ở Đường Lâm. Nhân dân các vùng xung quanh nổi dậy hưởng ứng và giành được quyền làm chủ vùng đất của mình.
- Ít lâu sau, Phùng Hưng kéo quân về bao vây phủ thành Tống Bình. Viên đô lộ là Cao Chính Bình phải rút vào thành cố thủ, rồi sinh bệnh chết. Phùng Hưng chiếm được thành, sắp đặt việc cai trị.
- Sau khi Phùng Hưng qua đời, con trai ông là Phùng An nối nghiệp.
- Năm 791, nhà Đường đem quân sang đàn áp, Phùng An ra hàng.

Gọi 5 số nguyên cần tìm là a, b, c, d, e.
Theo đề bài, ta có:
--> a + b = -6 (1)
--> b + c = -6 (2)
--> c + d = -6 (3)
--> d + e = -6 (4)
--> e + a = -6 (5)
Cộng (1), (2), (3), (4), (5), ta được:
--> 2(a + b + c + d + e) = -30
--> a + b + c + d + e = -15
Mặt khác, ta lại có:
-->  a + b + c + d + e = (a + b) + (c + d) + e = -6 + (-6) + e = -12 + e
Do đó, e = -15 - (-12) = -3.
Thay e = -3 vào (5), ta được:
--> a - 3 = -6
--> a = -3
Thay a = -3 vào (1), ta được:
--> -3 + b = -6
--> b = -3
Thay b = -3 vào (2), ta được:
--> -3 + c = -6
--> c = -3
Thay c = -3 vào (3), ta được:
--> -3 + d = -6
--> d = -3
Vậy 5 số nguyên cần tìm là -3, -3, -3, -3, -3.

a: Trên tia Ox, ta có: OA<OB

nên A nằm giữa O và B

=>OA+AB=OB

=>AB+5=10

=>AB=5(cm)

b: Vì A nằm giữa O và B

và OA=AB

nên A là trung điểm của OB

c: Vì OB và OC là hai tia đối nhau

nên O nằm giữa B và C

=>BC=BO+CO=10+4=14(cm)

d: TH1: E nằm giữa B và C

=>BE+EC=BC

=>EC+1=14

=>EC=13(cm)

TH2: B nằm giữa E và C

=>BE+BC=EC

=>EC=1+14=15(cm)

EC = BC - BE = 14cm - 1cm = 13cm.
~~~~~~~~~~~~~~~~~~~~~~~~
- Độ dài BC = 14cm (tính ở câu c)

a.

$42(-45)-55(-42)=42(-45)+55.42=42(-45+55)=42.10=420$

b.

$(-2-3)^2-(-2)^8:(-2)^5=(-5)^2-(-2)^3=25-(-8)=33$
c.

$=\frac{1}{5}+\frac{3}{10}+\frac{3}{2}+\frac{4}{7}$

$=\frac{2}{10}+\frac{3}{10}+\frac{3}{2}+\frac{4}{7}$

$=\frac{5}{10}+\frac{3}{2}+\frac{4}{7}$
$=\frac{1}{2}+\frac{3}{2}+\frac{4}{7}=2+\frac{4}{7}=\frac{18}{7}$

d.

$=\frac{3}{22}-\frac{7}{15}-\frac{3}{22}+\frac{7}{15}-\frac{1}{2}$

$=(\frac{3}{22}-\frac{3}{22})+(\frac{-7}{15}+\frac{7}{15})-\frac{1}{2}$

$=0+0-\frac{1}{2}=\frac{-1}{2}$

e.

$=\frac{77}{12}: \frac{11}{4}+\frac{45}{4}.\frac{2}{15}$

$=\frac{7}{3}+\frac{3}{2}=\frac{23}{6}$

f.

$=\frac{-7}{11}(\frac{11}{19}+\frac{12}{19}-\frac{4}{19})$

$=\frac{-7}{11}.\frac{19}{19}=\frac{-7}{11}$
 

Lời giải:

$11\frac{3}{13}-(2\frac{4}{7}+5\frac{3}{13})=11\frac{3}{13}-5\frac{3}{13}-2\frac{4}{7}$

$=6-2\frac{4}{7}=4-\frac{4}{7}=\frac{24}{7}$

b) 146/13 - ( 18/7 + 68/13)

 = 146/13 - 710/91

 = 24/7 :))

a: \(42\cdot\left(-45\right)-55\cdot\left(-42\right)\)

\(=-42\cdot45+55\cdot42\)

\(=42\left(55-45\right)=42\cdot10=420\)

b: \(\left(-2-3\right)^2-\left(-2\right)^8:\left(-2\right)^5\)

\(=\left(-5\right)^2-\left(-2\right)^3\)

\(=25-\left(-8\right)=33\)

c: \(\dfrac{1}{5}-\dfrac{-3}{2}+\dfrac{4}{7}-\dfrac{3}{-10}\)

\(=\dfrac{1}{5}+\dfrac{3}{2}+\dfrac{3}{10}+\dfrac{4}{7}\)

\(=\dfrac{2+15+3}{10}+\dfrac{4}{7}=2+\dfrac{4}{7}=\dfrac{18}{7}\)

d: \(\dfrac{3}{22}-\left(\dfrac{7}{15}-\dfrac{-3}{22}\right)+\dfrac{7}{15}-\dfrac{1}{2}\)

\(=\dfrac{3}{22}-\dfrac{7}{15}+\dfrac{3}{22}+\dfrac{7}{15}-\dfrac{1}{2}\)

\(=\dfrac{3}{11}-\dfrac{1}{2}=\dfrac{-5}{22}\)

e: \(6\dfrac{5}{12}:2\dfrac{3}{4}+11\dfrac{1}{4}\cdot\left(\dfrac{1}{3}-\dfrac{1}{5}\right)\)

\(=\dfrac{77}{12}:\dfrac{11}{4}+\dfrac{45}{4}\cdot\dfrac{2}{15}\)

\(=\dfrac{77}{12}\cdot\dfrac{4}{11}+\dfrac{45}{15}\cdot\dfrac{2}{4}\)

\(=\dfrac{7}{3}+\dfrac{3}{2}=\dfrac{23}{6}\)

f: \(\dfrac{-7}{11}\cdot\dfrac{11}{19}+\dfrac{-7}{11}\cdot\dfrac{12}{19}-\dfrac{4}{19}\cdot\dfrac{-7}{11}\)

\(=\dfrac{-7}{11}\left(\dfrac{11}{19}+\dfrac{12}{19}-\dfrac{4}{19}\right)\)

\(=\dfrac{-7}{11}\cdot1=-\dfrac{7}{11}\)

C = \(\dfrac{2}{3.5}\) + \(\dfrac{2}{5.7}\) + ... + \(\dfrac{2}{99.101}\)

C = \(\dfrac{1}{3}\) - \(\dfrac{1}{5}\) + \(\dfrac{1}{5}\) - \(\dfrac{1}{7}\) + ... + \(\dfrac{1}{99}\) - \(\dfrac{1}{101}\)

C = \(\dfrac{1}{3}\) - \(\dfrac{1}{101}\)

C = \(\dfrac{98}{303}\)

1 My father usually goes to work by car

2 How much does this hat cost?

3 What about singing an English song?

4 This is the oldes house in the village

5 The toy store is to the left of the book store

6 Badminon is Mai's favorite sport

7 We should plant more trees on the planet

8 How often do you go to the museum?

9 It will be sunny in the north tomorrow

10 Because she was late, she couldn't meet her music ido