trong mặt phẳng tọa độ Oxy, cho parabol (P): y=x^2 và đường thẳng (d): y=(m-3)x-m+4
a) Chứng minh đường thẳng (d) luôn đi qua điểm A(1;1) với mọi giá trị của m
b) Tìm m để (d) cắt (P) tại hai điểm phân biệt x1,x2 là dộ dài 2 cạnh của một tam giác vuông cân
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số dãy ghế ban đầu là \(x\left(x\inℕ^∗,x\le238\right)\) thì số ghế mỗi dãy là \(\dfrac{238}{x}\) \(\Rightarrow238⋮x\) \(\Rightarrow x\in\left\{1,2,7,14,17,34,119,238\right\}\)
Theo đề bài, ta có:
\(\left(x+3\right)\left(\dfrac{238}{x}-3\right)=238\)
\(\Leftrightarrow238-3x+\dfrac{714}{x}-9=238\)
\(\Leftrightarrow3x-\dfrac{714}{x}+9=0\)
\(\Leftrightarrow x^2+3x-238=0\)
\(\Leftrightarrow\left(x+17\right)\left(x-14\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-17\left(loại\right)\\x=14\left(nhận\right)\end{matrix}\right.\)
Vậy ban đầu phòng họp được chia làm 14 dãy ghế.

Ba phần tư giá niêm yết là:
\(300\text{ }000.\dfrac{3}{4}=225\text{ }000\) (đồng)
Giá gốc của chiếc áo là:
\(225\text{ }000:\left(100\%+25\%\right)=180\text{ }000\) (đồng)
Gọi x (đồng) là giá niêm yết để cửa hàng lãi 40%, ta có:
\(\dfrac{x-180\text{ }000}{180\text{ }000}.100\%=40\%\)
\(\Leftrightarrow x-180\text{ }000=72\text{ }000\)
\(\Leftrightarrow x=252\text{ }000\) (đồng)
Giải:
Giá chiếc áo nếu chỉ bán bằng \(\dfrac{3}{4}\) giá niêm yết là:
300 000 x \(\dfrac{3}{4}\) = 225 000 (đồng)
225 000 đồng ứng với:
100% + 25% = 125% (giá gốc)
Giá gốc của chiếc áo là:
225 000 : 125 x 100 = 180 000 (đồng)
Để lãi 40% giá gốc thì cần bán chiếc áo với giá là:
180 000 x (100% + 40%) = 252 000 (đồng)
Kết luận:...

Hỏi ban đầu phòng họp được chi là sao em nhỉ?

\(\Delta=m^2-4\left(m-2\right)=\left(m-2\right)^2+4>0;\forall m\)
Pt luôn có 2 nghiệm pb với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=m-2\end{matrix}\right.\)
Do \(x_2\) là nghiệm của pt nên: \(x_2^2-mx_2+m-2=0\)
\(\Rightarrow x_2^2=mx_2-\left(m-2\right)\)
\(\Rightarrow x_2^3=mx_2^2-\left(m-2\right)x_2\)
Thay vào bài toán:
\(mx_1^2+mx_2^2-\left(m-2\right)x_2+\left(m-2\right)x_2=3\)
\(\Leftrightarrow m\left(x_1^2+x_2^2\right)=3\)
\(\Leftrightarrow m\left[\left(x_1+x_2\right)^2-2x_1x_2\right]=3\)
\(\Leftrightarrow m\left(m^2-2\left(m-2\right)\right)=3\)
\(\Leftrightarrow m^3-2m^2+4m-3=0\)
\(\Leftrightarrow\left(m-1\right)\left(m^2-m+3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}m=1\\m^2-m+3=0\left(vn\right)\end{matrix}\right.\)

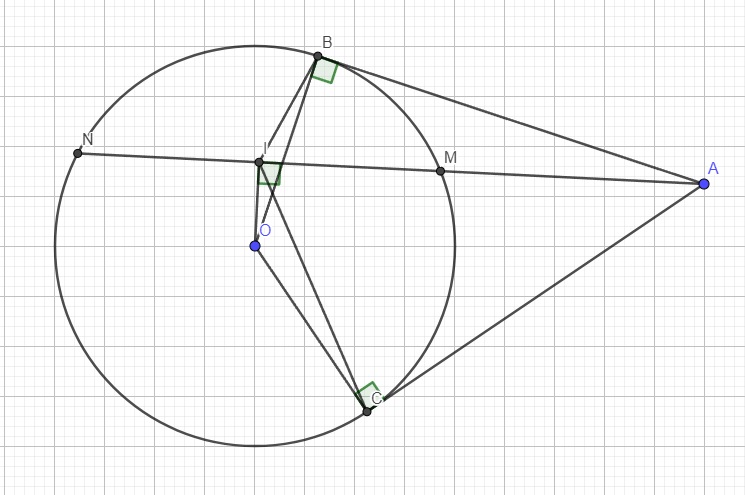
Do I là trung điểm MN \(\Rightarrow OI\perp MN\) \(\Rightarrow\widehat{OIA}=90^0\)
Do AB, AC là các tiếp tuyến \(\Rightarrow\widehat{OBA}=\widehat{OCA}=90^0\)
\(\Rightarrow I,B,C\) cùng nhìn OA dưới 1 góc vuông nên 5 điểm O, I, B, A, C cùng thuộc 1 đường tròn đường kính OA
Theo t/c 2 tiếp tuyến cắt nhau ta có: \(AB=AC\)
\(\Rightarrow\widehat{BIA}=\widehat{CIA}\) (2 góc nt chắn 2 cung bằng nhau của đường trònđường kính OA)
\(\Rightarrow IA\) là phân giác của BIC

I K Q O P H
Xét (O) có
sđ cung IQ = sđ cung KQ (gt)
=> IQ=KQ => tg IQK cân tại Q
OI=OK (bán kính (O))
\(\Rightarrow OQ\perp IK\) (trong tam giác cân đường trung tuyến xp từ đỉnh tg cân đồng thời là đường cao)
\(\Rightarrow\widehat{QOK}=90^o\)
Ta có
\(\widehat{IPK}=90^o\) (góc nội tiếp chắn nửa đường tròn)
=> O và P cùng nhìn HK dưới 2 góc bằng nhau và bằng 90 độ
=> O và P thuộc đường tròn đường kính HK => OKPH là tứ giác nội tiếp
b/
Xét tg HIK có
\(OH\perp IK;OI=OK\) => tg HIK cân tại H (tam giác có đường cao đồng thời là đường trung tuyến thì đó là tg cân)
\(\Rightarrow\widehat{KIP}=\widehat{HKI}\) (góc ở đáy tg cân)
Ta có
\(\widehat{PHK}=\widehat{KIP}+\widehat{HKI}\) (trong tg góc ngoài bằng tổng 2 góc trong không kề với nó)
\(\Rightarrow\widehat{PHK}=2\widehat{KIP}\Rightarrow\widehat{KIP}=\dfrac{1}{2}\widehat{PHK}\)

Câu 10:
\(\text{Δ}=\left(-2m\right)^2-4\cdot1\cdot\left(4m-3\right)\)
\(=4m^2-16m+12=4\left(m^2-4m+3\right)=4\left(m-3\right)\left(m-1\right)\)
Để phương trình có hai nghiệm phân biệt thì Δ>0
=>4(m-3)(m-1)>0
=>(m-3)(m-1)>0
=>\(\left[{}\begin{matrix}m>3\\m< 1\end{matrix}\right.\)

\(x^2-2mx+4m-3=0\) (1)
Ta có \(\Delta'=\left(-1\right)^2-\left(4m-3\right)=1-4m+3=-4m+4\)
Phương trình (1) có 2 nghiệm phân biệt => \(\Delta'>0\Leftrightarrow-4m+4>0\)
\(\Leftrightarrow4>4m\\ \Leftrightarrow1>m\)
Vậy phương trình có 2 nghiệm phân biệt khi m < 1
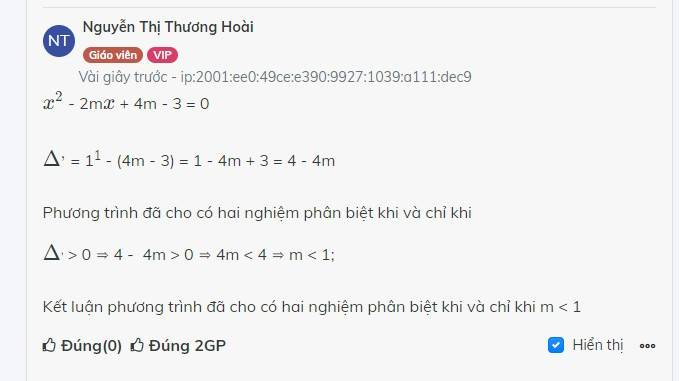
\(x^2\) - 2m\(x\) + 4m - 3 = 0
\(\Delta^,\) = 11 - (4m - 3) = 1 - 4m + 3 = 4 - 4m
Phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi
\(\Delta\), > 0 ⇒ 4 - 4m > 0 ⇒ 4m < 4 ⇒ m < 1;
Kết luận phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi m < 1


a: Thay x=1 và y=1 vào (d), ta được:
\(1\left(m-3\right)-m+4=1\)
=>m-3-m+4=1
=>1=1(luôn đúng)
Vậy: (d) luôn đi qua A(1;1)
b: Phương trình hoành độ giao điểm là:
\(x^2=\left(m-3\right)x-m+4\)
=>\(x^2-\left(m-3\right)x+m-4=0\)(1)
\(\text{Δ}=\left[-\left(m-3\right)\right]^2-4\cdot1\cdot\left(m-4\right)\)
\(=m^2-6m+9-4m+16=m^2-10m+25=\left(m-5\right)^2\)
Để (d) cắt (P) tại hai điểm phân biệt thì Δ>0
=>\(\left(m-5\right)^2>0\)
=>\(m-5\ne0\)
=>\(m\ne5\)
Khi m<>5 thì phương trình (1) sẽ có 2 nghiệm phân biệt là:
\(\left[{}\begin{matrix}x=\dfrac{m-3-\sqrt{\left(m-5\right)^2}}{2}=\dfrac{m-3-\left(m-5\right)}{2}=\dfrac{m-3-m+5}{2}=1\\x=\dfrac{m-3+\left(m-5\right)}{2}=\dfrac{2m-8}{2}=m-4\end{matrix}\right.\)
Để x1,x2 là độ dài 2 cạnh của một tam giác vuông cân thì m-4=1
=>m=5(loại)