1/1.2+1/2.3+...+1/1980.1990+...+2/2006.2007
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét tứ giác ABOC có \(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
nên ABOC là tứ giác nội tiếp
b: Xét (O) có
\(\widehat{ABN}\) là góc tạo bởi tiếp tuyến BA và dây cung BN
\(\widehat{BMN}\) là góc nội tiếp chắn cung BN
Do đó: \(\widehat{ABN}=\widehat{BMN}\)
Xét ΔABN và ΔAMB có
\(\widehat{ABN}=\widehat{AMB}\)
\(\widehat{BAN}\) chung
Do đó: ΔABN~ΔAMB
=>\(\dfrac{AB}{AM}=\dfrac{AN}{AB}\)
=>\(AB^2=AM\cdot AN\left(1\right)\)
Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(2)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(3)
Từ (2),(3) suy ra AO là trung trực của BC
=>AO\(\perp\)BC tại K
Xét ΔABO vuông tại B có BK là đường cao
nên \(AK\cdot AO=AB^2\left(4\right)\)
Từ (1),(4) suy ra \(AK\cdot AO=AN\cdot AM\)
=>\(\dfrac{AK}{AM}=\dfrac{AN}{AO}\)
Xét ΔAKN và ΔAMO có
\(\dfrac{AK}{AM}=\dfrac{AN}{AO}\)
\(\widehat{KAN}\) chung
Do đó: ΔAKN~ΔAMO
=>\(\widehat{AKN}=\widehat{AMO}\)
=>\(\widehat{AKN}=\widehat{OMN}\)
=>\(\widehat{AKN}=\widehat{ONM}\)

Giải:
Vì chuyển từ thùng nọ sang thùng kia nên tổng số dầu của hai thùng lúc sau không đổi và bằng 82 lít.
Ta có sơ đồ:
Theo sơ đồ ta có:
Số dầu thùng thứ nhất lúc sau là:
82 : 2 = 41 (l)
Số dầu thùng thứ nhất lúc dầu là:
41 + 7 = 48 (l)
Số dầu thùng thứ hai lúc đầu là:
82 - 48 = 34 (l)
Đáp số: Thùng thứ nhất lúc đầu có 48 l
Thùng thứ hai lúc đầu có 34 l

Đây là dạng toán nâng cao chuyên đề hai tỉ số tổng không đổi, cấu trúc thi chuyên, thi học sinh giỏi, thi violympic. Hôm nay Olm sẽ hướng dẫn câc em giải chi tiết dạng này như sau:
Giải:
Số học sinh nam lớp 5A luôn không đổi.
Số học sinh nữ lúc đầu bằng: 1 : 2 = \(\dfrac{1}{2}\) (số học sinh nam)
Số học sinh nữ lúc sau bằng: 1: \(\dfrac{5}{2}\) = \(\dfrac{2}{5}\) (số học sinh nam )
2 học sinh ứng với phân số là: \(\dfrac{1}{2}-\dfrac{2}{5}=\dfrac{1}{10}\) (số học sinh nam)
Số học sinh nam bằng: 2 : \(\dfrac{1}{10}=20\)(học sinh)
Số học sinh nữ lúc đầu là 20 x \(\dfrac{1}{2}\) = 10 (học sinh)
Ban đầu lớp đó có số học sinh là: 20 + 10 = 30 (học sinh)
Đáp số: 30 học sinh.

I:
Câu 1: \(M=\sqrt{9xy^2}=3\sqrt{xy^2}=3\sqrt{x}\cdot\left|y\right|=-3\sqrt{x}y\)
=>Chọn A
Câu 2: C
Câu 3: B
Câu 4: AC=AD+DC=4+8=12(cm)
Xét ΔBAC vuông tại B có BD là đường cao
nên \(BA^2=AD\cdot AC=4\cdot12=48\)
=>\(BA=4\sqrt{3}\left(cm\right)\)
=>Chọn D
II: Tự luận
Câu 5:
\(\left\{{}\begin{matrix}3x-2y=9\\x-3y=10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x-2y=9\\3x-9y=30\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-2y-3x+9y=9-30\\x-3y=10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}7y=-21\\x=3y+10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-3\\x=3\cdot\left(-3\right)+10=10-9=1\end{matrix}\right.\)
Câu 7:
a: \(\text{Δ}=3^2-4\cdot1\cdot\left(m+1\right)\)
=9-4m-4
=-4m+5
Để phương trình có nghiệm thì Δ>=0
=>-4m+5>=0
=>-4m>=-5
=>m<=5/4
b: Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-3\\x_1x_2=\dfrac{c}{a}=m+1\end{matrix}\right.\)
\(A=\left(x_1-x_2\right)^2+5x_1x_2+7m\)
\(=\left(x_1+x_2\right)^2-4x_1x_2+5x_1x_2+7m\)
\(=\left(-3\right)^2+\left(m+1\right)+7m=8m+10\)
=>A không có giá trị lớn nhất

Câu 6:
a: \(P=\dfrac{\sqrt{x}}{\sqrt{x}+2}+\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-\dfrac{2+5\sqrt{x}}{x-4}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}+2}+\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-\dfrac{5\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)+\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)-5\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{x-2\sqrt{x}+x+3\sqrt{x}+2-5\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{2x-4\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{2\sqrt{x}}{\sqrt{x}+2}\)
b: P>1
=>P-1>0
=>\(\dfrac{2\sqrt{x}-\sqrt{x}-2}{\sqrt{x}+2}>0\)
=>\(\dfrac{\sqrt{x}-2}{\sqrt{x}+2}>0\)
=>\(\sqrt{x}-2>0\)
=>x>4
Câu 9:
a: Xét tứ giác CEHF có \(\widehat{CEH}+\widehat{CFH}=90^0+90^0=180^0\)
nên CEHF là tứ giác nội tiếp
b: Xét ΔABC có
BF,AE là các đường cao
BF cắt AE tại H
Do đó: H là trực tâm của ΔABC
=>CH\(\perp\)AB
Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
=>BD\(\perp\)BA
mà CH\(\perp\)BA
nên CH//BD
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>AC\(\perp\)CD
mà BH\(\perp\)AC
nên BH//CD
Xét tứ giác BHCD có
BH//CD
BD//CH
Do đó: BHCD là hình bình hành

Bài 3
2b) ∆' = m² - 1.(2m - 1)
= m² - 2m + 1
= (m - 1)² > 0 với mọi m 1
Để phương trình có hai nghiệm phân biệt thỏa mãn x₁ ≤ 0 < x₂ thì:
x₁x₂ ≤ 0
⇔ 2m - 1 ≤ 0
⇔ 2m ≤ 1
⇔ m ≤ 1/2 (nhận)
Vậy m ≤ 1/2 thì phương trình có hai nghiệm thỏa mãn yêu cầu đề bài

ĐKXĐ: \(\left[{}\begin{matrix}x>=2\\x< =-2\end{matrix}\right.\)
\(\dfrac{1}{4}\sqrt{x^2-4}>=0\forall x\) thỏa mãn ĐKXĐ
=>\(-\dfrac{1}{4}\sqrt{x^2-4}< =0\forall x\) thỏa mãn ĐKXĐ
=>\(-\dfrac{1}{4}\sqrt{x^2-4}+1< =1\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi \(x^2-4=0\)
=>\(x^2=4\)
=>\(\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)

\(\dfrac{1}{5}\) tấn \(56kg\) \(< 20kg\times34\)
\(\dfrac{3}{4}h< 8400s:3\)
\(\dfrac{1}{5}\) tấn 56 kg = 1000 kg x \(\dfrac{1}{5}\) + 56 kg = 256 kg
20 kg x 34 = 680 kg
Vì 256 kg < 680 kg
Vậy \(\dfrac{1}{5}\) tấn 56 kg < 20 kg x 34
\(\dfrac{3}{4}giờ\) = 3600 giây x \(\dfrac{3}{4}\) = 2700 giây
8400 giây: 3 = 2800 giây
Vì 2700 giây < 2800 giây
Vậy \(\dfrac{3}{4}\) giờ < 8400 giây : 3



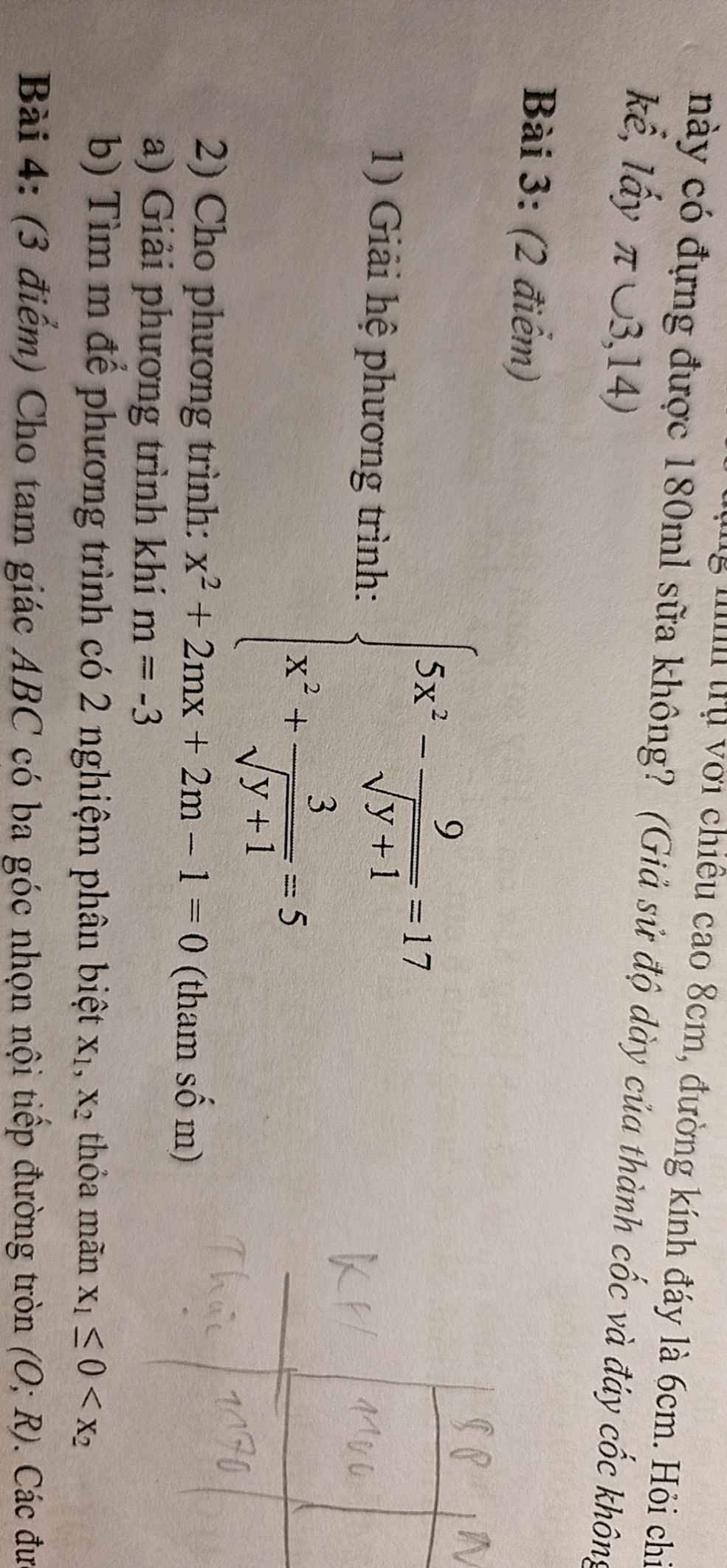
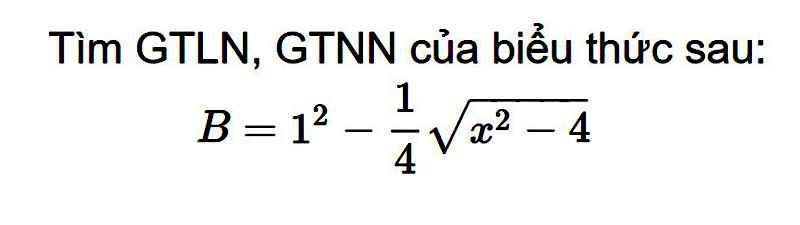
Em xem lại đề nhé. Các phân số này không có quy luật nên không tính được