a: Vì \(AB=\dfrac{1}{2}CD\) và AB//CD

nên \(\dfrac{S_{ABD}}{S_{BDC}}=\dfrac{AB}{DC}=\dfrac{1}{2}\)

=>\(S_{ABD}=\dfrac{1}{2}S_{BDC}\)

b:  Vì AB//CD

nên \(\dfrac{OB}{OD}=\dfrac{OA}{OC}=\dfrac{AB}{CD}=\dfrac{1}{2}\)

\(\Leftrightarrow OD=2OB;OC=2OA\)

Vì OD=2OB

nên \(S_{AOD}=2\times S_{AOB}\)

Vì OC=2OA

nên \(S_{BOC}=2\times S_{BOA}\)

Do đó: \(S_{AOD}=S_{BOC}\)

c: Vì OD=2OB

nên \(S_{AOD}=2\times S_{AOB}=8\left(cm^2\right)\)

=>\(S_{BOC}=8\left(cm^2\right)\)

Vì OC=2OA

nên \(S_{DOC}=2\times S_{AOD}=16\left(cm^2\right)\)

\(S_{ABCD}=S_{OBA}+S_{OBC}+S_{AOD}+S_{DOC}\)

\(=4+8+8+16=24+12=36\left(cm^2\right)\)

\(A=\dfrac{5-\dfrac{5}{2}+1-\dfrac{5}{8}+\dfrac{5}{11}}{11-\dfrac{11}{2}+\dfrac{11}{5}-\dfrac{11}{8}+1}\)

\(=\dfrac{5-\dfrac{5}{2}+\dfrac{5}{5}-\dfrac{5}{8}+\dfrac{5}{11}}{11-\dfrac{11}{2}+\dfrac{11}{5}-\dfrac{11}{8}+\dfrac{11}{11}}\)

\(=\dfrac{5\left(1-\dfrac{1}{2}+\dfrac{1}{5}-\dfrac{1}{8}+\dfrac{1}{11}\right)}{11\left(1-\dfrac{1}{2}+\dfrac{1}{5}-\dfrac{1}{8}+\dfrac{1}{11}\right)}=\dfrac{5}{11}\)

a = 5/11

a: Vận tốc khi ngược dòng là: 9:3/2=6(km/h)

b: Vận tốc của dòng nước là:

(9-6):2=1,5(km/h)

Vận tốc thật của thuyền là 1,5+6=7,5(km/h)

Độ dài quãng đường AB là:

\(1:\left(\dfrac{1}{6}+\dfrac{1}{9}\right)=1:\left(\dfrac{3}{18}+\dfrac{2}{18}\right)=\dfrac{18}{5}=3,6\left(km\right)\)

\(x\times4,9+x:10=24\)

=>\(x\times4,9+x\times0,1=24\)

=>\(x\times5=24\)

=>x=24:5=4,8

\(1,2-2,2+3,2-4,2+5,2-6,2+...+22,2-23,2+24,2\)

\(=\left(1,2-2.2\right)+\left(3,2-4,2\right)+\left(5,2-6,2\right)+...+\left(22,2-23,2\right)+24,2\)

\(=\left(-1\right)+\left(-1\right)+\left(-1\right)+...+\left(-1\right)+24,2\)

\(=\left(-1\right).23+24,2\)

\(=\left(-23\right)+24,2\)

\(=1,2\)

Ai trả lời nhanh nhất mình tặng 20 coin

Nhanh với ạ , mình đang cần rất gấp ạ

Những bạn học sinh gỏi đâu rồi

Những thầy cô yêu quý đâu ạ

a: Vì AB//CD

nên \(\dfrac{S_{ABC}}{S_{ADC}}=\dfrac{AB}{DC}=\dfrac{1}{3}\)

=>\(S_{ADC}=3\times S_{ABC}\)

\(S_{ABC}+S_{ADC}=S_{ABCD}\)

=>\(4\times S_{ABC}=24\)

=>\(S_{ABC}=6\left(cm^2\right)\)

b: Vì AB//CD

nên ΔMAB~ΔMDC

=>\(\dfrac{S_{MAB}}{S_{MDC}}=\left(\dfrac{AB}{CD}\right)^2=\dfrac{1}{9}\)

=>\(\dfrac{S_{MAB}}{S_{ABCD}}=\dfrac{1}{8}\)

=>\(S_{MAB}=\dfrac{S_{ABCD}}{8}=\dfrac{24}{8}=3\left(cm^2\right)\)

Anh có hình ko ạ ?

a: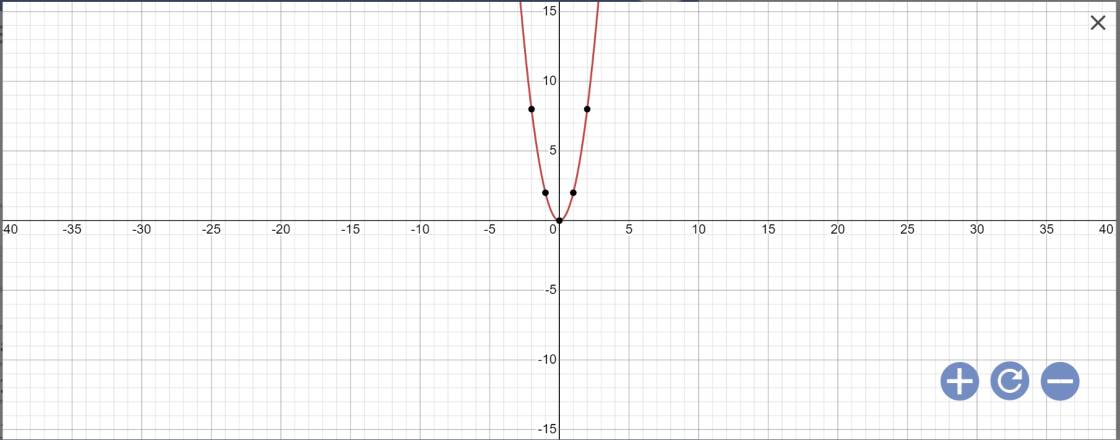 

b: Phương trình hoành độ giao điểm là:

\(2x^2=3x-1\)

=>\(2x^2-3x+1=0\)

=>(x-1)(2x-1)=0

=>\(\left[{}\begin{matrix}x=1\\x=\dfrac{1}{2}\end{matrix}\right.\)

Khi x=1 thì \(y=2\cdot x^2=2\cdot1^2=2\)

Khi x=1/2 thì \(y=2\cdot\left(\dfrac{1}{2}\right)^2=\dfrac{1}{2}\)

Vậy: (P) giao (Δ) tại A(1;2); B(1/2;1/2)

c: Phương trình hoành độ giao điểm là:

\(2x^2=-2\left(m-2\right)x-2m+6\)

=>\(2x^2+2\left(m-2\right)x+2m-6=0\)

=>\(x^2+\left(m-2\right)x+m-3=0\)

\(\text{Δ}=\left(m-2\right)^2-4\left(m-3\right)\)

\(=m^2-4m+4-4m+12=m^2-8m+16=\left(m-4\right)^2\)

Để (d) cắt (P) tại hai điểm phân biệt thì Δ>0

=>\(\left(m-4\right)^2>0\)

=>\(m-4\ne0\)

=>\(m\ne4\)

Theo Vi-et, ta có:

\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-m+2\\x_1x_2=\dfrac{c}{a}=m-3\end{matrix}\right.\)

\(2x_1x_2-\left(x_1-x_2\right)^2=-1\)

=>\(2x_1x_2-\left[\left(x_1+x_2\right)^2-4x_1x_2\right]=-1\)

=>\(-\left(x_1+x_2\right)^2+6x_1x_2=-1\)

=>\(-\left(-m+2\right)^2+6\left(m-3\right)=-1\)

=>\(-m^2+4m-4+6m-18+1=0\)

=>\(-m^2+10m-21=0\)

=>\(\left(m-3\right)\left(m-7\right)=0\)

=>\(\left[{}\begin{matrix}m=3\left(nhận\right)\\m=7\left(nhận\right)\end{matrix}\right.\)

a/ S(ABNP)= 36*36/2; S(PAM)+S(NBM)= 24*12; S(MNP)= S(ABNP) - S(PAM) - S(NBM) = 360cm2

360cm2

b/240cm2