
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Áp dụng BĐT Bunhiacopxky:
$(14x^2-4x+6).16=[(x-2)^2+x^2+12x^2+2][1+1+12+1]\geq [(2-x)+x+12x+2]^2=(12x+4)^2$
$\Rightarrow 14x^2-4x+6\geq (3x+1)^2$
$\Rightarrow \sqrt{14x^2-4x+6}\geq |3x+1|$
$\Rightarrow A\geq |3x+1|+|3x-4|+2019$
Mà:
$|3x+1|+|3x-4|=|3x+1|+|4-3x|\geq |3x+1+4-3x|=5$
$\Rightarrow A\geq 5+2019=2024$
Vậy $A_{\min}=2024$
Giá trị này xảy ra khi $x=1$

a: Xét tứ giác MAOH có \(\widehat{MAO}+\widehat{MHO}=90^0+90^0=180^0\)
nên MAOH là tứ giác nội tiếp
b: Xét ΔAMB vuông tại A và ΔAON vuông tại A có
\(\widehat{AMB}=\widehat{AON}\left(=90^0-\widehat{ANO}\right)\)
Do đó: ΔAMB~ΔAON
=>\(\dfrac{AM}{AO}=\dfrac{AB}{AN}\)
=>\(AM\cdot AN=AO\cdot AB\)


Lời giải:
Gọi giá ban đầu của 1 hộp sữa là $a$ và giá 1 gói đường là $b$ (đồng)
Theo bài ra ta có:
\(\left\{\begin{matrix}\\ 9a+3b=147000\\ 9(a-1500)+3b.0,9=147000-21000\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}\\ 9a+3b=147000\\ 9a+2,7b=139500\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}\\ a=8000\\ b=25000\end{matrix}\right.\)

Diện tích mảnh vườn là:
\(1200000:20000=60\left(m^2\right)\)
Gọi chiều rộng mảnh vườn là x (m) với x>0
Chiều dài mảnh vườn là: \(x+4\) (m)
Diện tích mảnh vườn là: \(x\left(x+4\right)\) \(\left(m^2\right)\)
Do diện tích mảnh vườn là 60 \(m^2\) nên ta có pt:
\(x\left(x+4\right)=60\)
\(\Leftrightarrow x^2+4x-60=0\Rightarrow\left[{}\begin{matrix}x=6\\x=-10\left(loại\right)\end{matrix}\right.\)
Vậy mảnh vườn rộng 6m

Gọi vận tốc cano lúc ngược dòng là x (km/h)
Vận tốc cano lúc xuôi dòng là: \(x+6\) (km/h)
Thời gian cano xuôi dòng là: \(\dfrac{90}{x+6}\) giờ
Thời gian cano ngược dòng là: \(\dfrac{63}{x}\) giờ
Do thời gian xuôi dòng ít hơn thời gian ngược dòng 1 giờ nên ta có pt:
\(\dfrac{63}{x}-\dfrac{90}{x+6}=1\)
\(\Rightarrow63\left(x+6\right)-90x=x\left(x+6\right)\)
\(\Leftrightarrow x^2+33x-378=0\Rightarrow\left[{}\begin{matrix}x=9\\x=-42\left(loại\right)\end{matrix}\right.\)
Vậy cano xuôi dòng với vận tốc 15km/h và ngược dòng với vận tốc 9km/h

1: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đó: ΔADB vuông tại D
Xét tứ giác BCKH có \(\widehat{BCK}+\widehat{BHK}=90^0+90^0=180^0\)
nên BCKH là tứ giác nội tiếp
b: Xét ΔAHK vuông tại H và ΔACB vuông tại C có
\(\widehat{HAK}\) chung
Do đó: ΔAHK~ΔACB
=>\(\dfrac{AH}{AC}=\dfrac{AK}{AB}\)
=>\(AK\cdot AC=AH\cdot AB\)
Xét ΔBHK vuông tại H và ΔBDA vuông tại D có
\(\widehat{HBK}\) chung
Do đó: ΔBHK~ΔBDA
=>\(\dfrac{BH}{BD}=\dfrac{BK}{BA}\)
=>\(BH\cdot BA=BK\cdot BD\)
\(AK\cdot AC+BK\cdot BD\)
\(=AH\cdot AB+BH\cdot AB=AB\left(BH+AH\right)=AB^2=4R^2\)

a: Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đó: ΔADB vuông tại D
=>AD\(\perp\)DB tại D
Xét (O) có
SA,SD là các tiếp tuyến
Do đó: SA=SD
=>S nằm trên đường trung trực của AD(1)
ta có: OA=OD
=>O nằm trên đường trung trực của AD(2)
Từ (1),(2) suy ra SOlà đường trung trực của AD
=>SO\(\perp\)AD
Ta có: SO\(\perp\)AD
AD\(\perp\)DB
Do đó: SO//DB
b: Ta có: ΔADB vuông tại D
=>ΔADC vuông tại D
Ta có: \(\widehat{SAD}+\widehat{SCD}=90^0\)(ΔACD vuông tại D)
\(\widehat{SDA}+\widehat{SDC}=\widehat{ADC}=90^0\)
mà \(\widehat{SAD}=\widehat{SDA}\)(ΔSAD cân tại S)
nên \(\widehat{SCD}=\widehat{SDC}\)
=>SC=SD
=>SC=SA(3)
c: Ta có: DH\(\perp\)AB
CA\(\perp\)AB
Do đó: DH//CA
Xét ΔBCS có DE//CS
nên \(\dfrac{DE}{SC}=\dfrac{BE}{BS}\left(4\right)\)
Xét ΔBAS có EH//SA
nên \(\dfrac{EH}{SA}=\dfrac{BE}{BS}\left(5\right)\)
Từ (3),(4),(5) suy ra DE=EH
=>E là trung điểm của DH

a: Xét tứ giác BFEC có \(\widehat{BFC}=\widehat{BEC}=90^0\)
nên BFEC là tứ giác nội tiếp đường tròn đường kính BC
Xét (O) có
\(\widehat{CPQ}\) là góc nội tiếp chắn cung CQ
\(\widehat{CBQ}\) là góc nội tiếp chắn cung CQ
Do đó: \(\widehat{CPQ}=\widehat{CBQ}\)
=>\(\widehat{HPQ}=\widehat{HFE}\)
=>PQ//FE
b: Vì BFEC là tứ giác nội tiếp đường tròn đường kính BC
nên BFEC nội tiếp (I)
=>IF=IE=IB=IC
Xét ΔICE có \(\widehat{EIB}\) là góc ngoài tại đỉnh I
nên \(\widehat{EIB}=\widehat{IEC}+\widehat{ICE}=2\cdot\widehat{ACB}\)
Xét tứ giác AFDC có \(\widehat{AFC}=\widehat{ADC}=90^0\)
nên AFDC là tứ giác nội tiếp
=>\(\widehat{BFD}=\widehat{BCA}\left(=180^0-\widehat{AFD}\right)\)
Vì BFEC là tứ giác nội tiếp
nên \(\widehat{AFE}=\widehat{ACB}\left(=180^0-\widehat{EFB}\right)\)
\(\widehat{AFE}+\widehat{EFD}+\widehat{BFD}=180^0\)
=>\(\widehat{EFD}+\widehat{ACB}+\widehat{ACB}=180^0\)
=>\(\widehat{EFD}+2\cdot\widehat{ACB}=180^0\)
=>\(\widehat{EFD}+\widehat{EID}=180^0\)
=>EFDI là tứ giác nội tiếp
=>\(\widehat{FDE}=\widehat{FIE}\)
Xét (I) có
\(\widehat{FCE}\) là góc nội tiếp chắn cung FE
nên \(\widehat{FCE}=\dfrac{\widehat{FIE}}{2}\)
=>\(\widehat{FIE}=2\cdot\widehat{FCE}=2\cdot\widehat{ACF}=2\cdot\widehat{ABE}\)
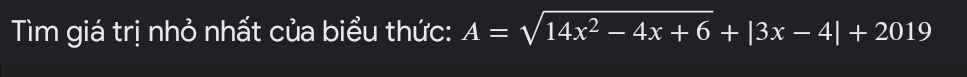
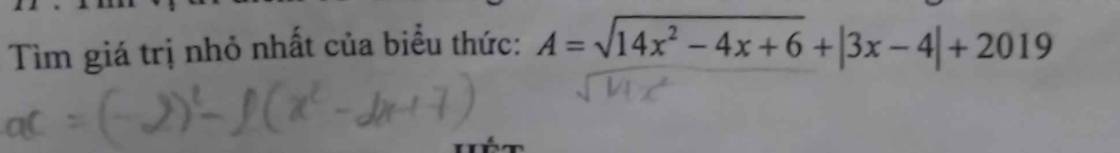

Lời giải:
$A=\sqrt{8}-\sqrt{2}=\sqrt{2^2.2}-\sqrt{2}=2\sqrt{2}-\sqrt{2}=\sqrt{2}$
$B=\frac{a+2\sqrt{a}}{\sqrt{a}+2}=\frac{\sqrt{a}(\sqrt{a}+2)}{\sqrt{a}+2}=\sqrt{a}$