Một cửa hàng bán một số mét vải trong ba ngày. Ngày thứ nhất bán \(\dfrac{3}{5}\) số mét vải. Ngày thứ hai bán \(\dfrac{2}{7}\) số mét vải còn lại. Ngày thứ ba bán nốt 40 mét vải. Tính tổng số mét vải cửa hàng đã bán
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giải:
Số cây ngày thứ nhất lớp 6A trồng được là:
\(56\cdot\dfrac{3}{8}=21\left(\text{cây}\right)\)
Số cây ngày thứ hai lớp 6A trồng được là:
\(\left(56-21\right)\cdot\dfrac{4}{7}=20\left(\text{cây}\right)\)
Số cây ngày thứ ba lớp 6A trồng được là:
\(56-21-20=15\left(\text{cây}\right)\)
Vậy ....

Độ dài quãng đường ô tô đi được trong giờ thứ nhất là:
\(120\cdot\dfrac{1}{3}=40\left(km\right)\)
Độ dài quãng đường còn lại là 120-40=80(km)
Độ dài quãng đường ô tô đi được trong giờ thứ ba là:
\(80\left(1-40\%\right)=48\left(km\right)\)

Chiều rộng của bể nước là \(1,6\cdot\dfrac{3}{4}=1,2\left(m\right)\)
Chiều dài bể nước là \(1,2\cdot150\%=1,8\left(m\right)\)
Thể tích của bể là:
\(1,6\cdot1,2\cdot1,8=3,456\left(m^3\right)\)
Chiều rộng bể nước là:
\(1,6\times\dfrac{3}{4}=1,2\) ( m )
Chiều dài bể nước là::
\(1,2\times150\%=1,8\) ( m )
Thể tích của bể nước là:
\(1,8\times1,2\times1,6=3,456\) ( m3 )
Đ/S:....

2,3*456=2,3(450+6)
\(=2,3\cdot450+2,3\cdot6\)
\(=1035+13,8=1048,8\)

\(\left(-0,4\right)\cdot\left(-0,5\right)\cdot\left(-0,2\right)\)
\(=-0,4\cdot0,5\cdot0,2\)
\(=-0,2\cdot0,2=-0,04\)

a: \(\dfrac{3}{5}+3\dfrac{5}{6}\left(11\dfrac{5}{20}-9\dfrac{1}{4}\right):7\dfrac{2}{3}\)
\(=\dfrac{3}{5}+\dfrac{23}{6}\left(11+\dfrac{5}{20}-9-\dfrac{1}{4}\right):\dfrac{23}{3}\)
\(=\dfrac{3}{5}+\dfrac{23}{6}\cdot2\cdot\dfrac{3}{23}=\dfrac{3}{5}+1=\dfrac{8}{5}\)
b: \(\dfrac{7}{13}\cdot\dfrac{7}{15}-\dfrac{1}{3}\cdot\dfrac{21}{39}+\dfrac{49}{91}\cdot\dfrac{8}{15}\)
\(=\dfrac{7}{13}\cdot\dfrac{7}{15}-\dfrac{1}{3}\cdot\dfrac{7}{13}+\dfrac{7}{13}\cdot\dfrac{8}{15}\)
\(=\dfrac{7}{13}\left(\dfrac{7}{15}+\dfrac{8}{15}-\dfrac{1}{3}\right)=\dfrac{7}{13}\cdot\dfrac{2}{3}=\dfrac{14}{39}\)
c: \(\left(1-\dfrac{1}{2}\right)\left(1-\dfrac{1}{3}\right)\cdot...\cdot\left(1-\dfrac{1}{2023}\right)\)
\(=\dfrac{1}{2}\cdot\dfrac{2}{3}\cdot...\cdot\dfrac{2022}{2023}\)
\(=\dfrac{1}{2023}\)
d: \(\dfrac{2}{4\cdot5}+\dfrac{2}{5\cdot6}+...+\dfrac{2}{99\cdot100}\)
\(=2\left(\dfrac{1}{4\cdot5}+\dfrac{1}{5\cdot6}+...+\dfrac{1}{99\cdot100}\right)\)
\(=2\left(\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+...+\dfrac{1}{99}-\dfrac{1}{100}\right)\)
\(=2\left(\dfrac{1}{4}-\dfrac{1}{100}\right)=2\cdot\dfrac{24}{100}=\dfrac{48}{100}=\dfrac{12}{25}\)
e: \(\dfrac{3}{1\cdot3}+\dfrac{3}{3\cdot5}+...+\dfrac{3}{99\cdot101}\)
\(=\dfrac{3}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{99\cdot101}\right)\)
\(=\dfrac{3}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{99}-\dfrac{1}{101}\right)\)
\(=\dfrac{3}{2}\left(1-\dfrac{1}{101}\right)=\dfrac{3}{2}\cdot\dfrac{100}{101}=\dfrac{150}{101}\)
f: \(\dfrac{10}{3\cdot6}+\dfrac{10}{6\cdot9}+...+\dfrac{10}{96\cdot99}\)
\(=\dfrac{10}{3}\left(\dfrac{3}{3\cdot6}+\dfrac{3}{6\cdot9}+...+\dfrac{3}{96\cdot99}\right)\)
\(=\dfrac{10}{3}\left(\dfrac{1}{3}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{9}+...+\dfrac{1}{96}-\dfrac{1}{99}\right)\)
\(=\dfrac{10}{3}\left(\dfrac{1}{3}-\dfrac{1}{99}\right)=\dfrac{10}{3}\cdot\dfrac{32}{99}=\dfrac{320}{297}\)

A=1.21+3.41+5.61+...+49.501
𝐴=(1+13+15+...+149)−(12+14+...+150)A=(1+31+51+...+491)−(21+41+...+501)
𝐴=(1+12+13+14+15+16+...+149+150)−2(12+14+...+150)A=(1+21+31+41+51+61+...+491+501)−2(21+41+...+501)
𝐴=(1+12+13+14+15+16+...+149+150)−(1+12+13+...+125)A=(1+21+31+41+51+61+...+491+501)−(1+21+31+...+251)
𝐴=126+127+...+149+150<126+126+126+...+126=2526<1.A=261+271+...+491+501<261+261+261+...+261=2625<1.

Kim ngạch xuất khẩu của Việt Nam với thị trường châu Âu là:
135,45-88,18=47,27(tỉ USD)
Kim ngạch xuất khẩu của Việt Nam với thị trường Mỹ là:
\(156,32\%\cdot47,27\simeq73,89\left(tỉUSD\right)\)
Kim ngạch xuất khẩu của Việt nam với thị trường châu Á nhiều hơn tổng 2 thị trường kia là:
135,45-(47,27+73,89)\(\simeq\)14,29(tỉ USD)
Kim ngạch xuất khẩu của Việt Nam với thị trường châu Âu là:
135,45-88,18=47,27(tỉ USD)
Kim ngạch xuất khẩu của Việt Nam với thị trường Mỹ là:
156,32%⋅47,27≃73,89(�ỉ���)156,32%⋅47,27≃73,89(tỉ usd)
Kim ngạch xuất khẩu của Việt nam với thị trường châu Á nhiều hơn tổng 2 thị trường kia là:
135,45-(47,27+73,89)≃≃14,29(tỉ USD)
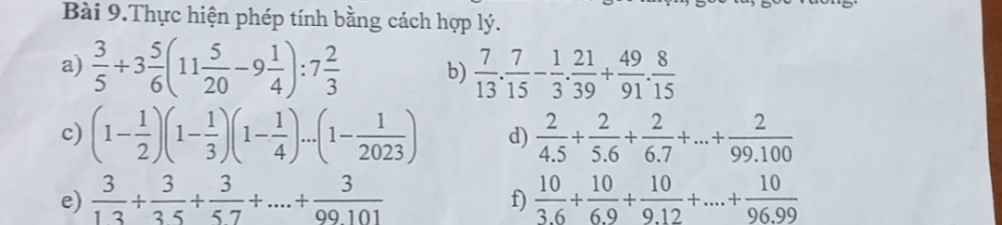
Phân số biểu thị số m vải bán trong ngày thứ ba là:
\(1-\dfrac{3}{5}-\dfrac{2}{7}=\dfrac{4}{35}\) ( số m vải )
Tổng số m vải cả ba ngày bán đc là:
\(40:\dfrac{4}{35}=350\) ( m vải )
Đ/S:....
350 m vải