Chúng ta cần tìm giá trị lớn nhất và giá trị nhỏ nhất của hai hàm số đã chọn. ### **Câu a: \( F = \frac{2x + 3}{x^2 + 4} \)** #### **Bước 1: Tìm đạo hàm của \( F \)** Gọi: \[ F(x) = \frac{2x + 3}{x^2 + 4} \] Đạo hàm của \( F(x) \) theo quy tắc kinh tế: \[ F'(x) = \frac{(2)(x^2+4) - (2x+3)(2x)}{(x^2+4)^2} \] \[ = \frac{2x^2 + 8 - (4x^2 + 6x)}{(x^2+4)^2} \] \[ = \frac{-2x^2 - 6x + 8}{(x^2+4)^2} \] #### **Bước 2: Tìm các điểm cực trị** Phương pháp giải thích: \[ -2x^2 - 6x + 8 = 0 \] Chia hai vế cho -2: \[ x^2 + 3x - 4 = 0 \] \[ (x + 4)(x - 1) = 0 \] \[ x = -4, x = 1 \] #### **Bước 3: chắc hạn tại \( x \to \pm\infty \)** \[ \lim_{x \to \pm\infty} F(x) = 0 \] #### **Bước 4: Tính giá trị của \( F(x) \) tại các cực trị và một số điểm đặc biệt**### **Câu a: Tìm giá trị lớn nhất, nhỏ nhất của \( F = \frac{2x + 3}{x^2 + 4} \)** #### **Bước 1: Tìm đạo hàm của \( F(x) \)** Sử dụng quy tắc đạo hàm của một phân thức: \[ F(x) = \frac{2x + 3}{x^2 + 4} \] áp dụng công thức: \[ F'(x) = \frac{(2)(x^2 + 4) - (2x + 3)(2x)}{(x^2 + 4)^2} \] \[ = \frac{2x^2 + 8 - (4x^2 + 6x)}{(x^2 + 4)^2} \] \[ = \frac{-2x^2 - 6x + 8}{(x^2 + 4)^2} \] #### **Bước 2: Tìm các cực trị** Giải thích phương trình \( F'(x) = 0 \): \[ -2x^2 - 6x + 8 = 0 \] Chia hai vế cho -2: \[ x^2 + 3x - 4 = 0 \] Phân tích thành nhân tử: \[ (x + 4)(x - 1) = 0 \] \[ x = -4, x = 1 \] #### **Bước 3: dừng giới hạn tại \( x \to \pm\infty \)** \[ \lim_{x \to \pm\infty} F(x) = 0 \] Do đó đồ thị có đỉnh ngang là \( y = 0 \). #### **Bước 4: Tính giá trị của \( F(x) \) tại các cực trị** \[ F(-4) =

Olm chào em, em xem hướng dẫn chi tiết dưới đây em sẽ hiểu vì sao em nhé.

Giải:

\(x^2\) - 5\(x\) + 6

= (\(x^2\) - 3\(x\)) - (2\(x-6\))

= \(x\left(x-3\right)-2\left(x-3\right)\)

= (\(x-3\))(\(x-2\))

Vì (x-3) (x-2)=x^2-5x+6

1: Để (d) cắt (d') tại một điểm trên trục tung thì

\(\left\{{}\begin{matrix}a\ne a'\\b=b'\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}m\ne m-2\\m-1=-2m\end{matrix}\right.\Leftrightarrow3m=1\)

=>\(m=\dfrac{1}{3}\)

2: Thay x=2 vào y=mx+m-1, ta được:

\(y=m\cdot2+m-1=3m-1\)

Thay x=2 và y=3m-1 vào (d'), ta được:

\(2\left(m-2\right)-2m=3m-1\)

=>3m-1=-4

=>3m=-3

=>m=-1

3: Thay x=-1 và y=2 vào (d), ta được:

\(m\cdot\left(-1\right)+m-1=2\)

=>-m+m-1=2

=>-1=2(vô lý)

vậy: \(m\in\varnothing\)

Giải:

Số trái cây sầu riêng cửa hàng đã bán được là:

400 x 20 : 100 = 80 (kg)

Kết luận số trái cây sầu riêng cửa hàng đã bán là 80 kg.

80kg

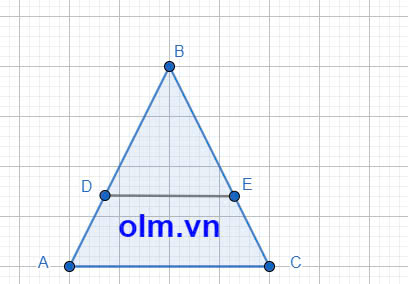
Các tỉ số theo định lí Thales là:

1; \(\frac{BD}{BA}\) = \(\frac{BE}{AC}\)

2; \(\frac{BD}{DA}\) = \(\frac{BE}{EC}\)

3; \(\frac{DA}{BA}\) = \(\frac{EC}{BC}\)

\(x^2-9x+8=0\)

=>\(x^2-x-8x+8=0\)

=>x(x-1)-8(x-1)=0

=>(x-1)(x-8)=0

=>\(\left[{}\begin{matrix}x-1=0\\x-8=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=8\end{matrix}\right.\)

x^2-9x+8=0

(x-8)(x-1)=0

x=8 hoặc x=1.

a: 2(a+b)-a+3b

=2a+2b-a+3b

=a+5b

b: 4(3a-4b)+5(2a+b)

=12a-16b+10a+5b

=12a+10a-16b+5b

=22a-11b

a: ta có; AM+MB=AB

BN+NC=BC

CP+PD=CD

DQ+QA=DA

mà AB=BC=CD=DA và AM=BN=CP=DQ

nên MB=NC=PD=QA

Xét ΔQAM vuông tại A và ΔNCP vuông tại C có

QA=NC

AM=CP

Do đó: ΔQAM=ΔNCP

b: ΔQAM=ΔNCP

=>QM=PN

Xét ΔMBN vuông tại B và ΔPDQ vuông tại D có

MB=PD

BN=DQ

Do đó: ΔMBN=ΔPDQ

=>MN=PQ

Xét ΔMAQ vuông tại A và ΔNBM vuông tại B có

MA=NB

AQ=BM

Do đó: ΔMAQ=ΔNBM

=>MQ=MN

Ta có: ΔMAQ=ΔNBM

=>\(\widehat{AMQ}=\widehat{BNM}\)

=>\(\widehat{AMQ}+\widehat{BMN}=90^0\)

Ta có: \(\widehat{AMQ}+\widehat{QMN}+\widehat{NMB}=180^0\)

=>\(\widehat{QMN}+90^0=180^0\)

=>\(\widehat{QMN}=90^0\)

Xét tứ giác MNPQ có

MN=PQ

MQ=PN

Do đó: MNPQ là hình bình hành

Hình bình hành MNPQ có MN=MQ

nên MNPQ là hình thoi

Hình thoi MNPQ có \(\widehat{QMN}=90^0\)

nên MNPQ là hình vuông

a) \(...\Rightarrow x\left(x^2-16\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2-16=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2=16\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\pm4\end{matrix}\right.\)

b) \(...\Rightarrow x\left(x^3-2x^2+10x-20\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^3-2x^2+10x-20=0\left(1\right)\end{matrix}\right.\)

\(\left(1\right)\Leftrightarrow\left(x-2\right)\left(x^2+10\right)=0\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x^2+10=0\left(vô.lý\right)\end{matrix}\right.\Leftrightarrow x=2\)

Vậy \(x\in\left\{0;2\right\}\)

c) \(...\Rightarrow\left[{}\begin{matrix}2x-3=x+5\\2x-3=-x-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\\3x=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-\dfrac{2}{3}\end{matrix}\right.\)

d) \(...\Rightarrow x^2\left(x-1\right)-4x\left(x-1\right)+4\left(x-1\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left(x^2-4x+4\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x^2-4x+4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(x-2\right)^2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)

a; \(x^3\) - 16\(x\) = 0

    \(x\)(\(x^2\) - 16) = 0

    \(\left[{}\begin{matrix}x=0\\x^2=16\end{matrix}\right.\)

    \(\left[{}\begin{matrix}x=0\\x^2=\left(-4\right)^2\end{matrix}\right.\)

     \(\left[{}\begin{matrix}x=0\\x=-4\\x=4\end{matrix}\right.\)

Vậy \(x\) \(\in\) {0; -4; 4}