Một nhà máy sản xuất ra được một số khẩu trang . Được đóng vào các gói mỗi gói 10 chiếc, biết rằng khi đóng vào các hộp, mỗi hộp 24 gói thì vừa đủ, đóng vào các hộp, mỗi hộp 45 chiếc thì vùa đủ và số khẩu trang chỉ từ 1000 cho đến 1200 chiếc
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi x (cm) là độ dài cạnh của lục giác đều (x > 0)
Ta có:
x . √3 = 25
x = 25/√3
Vậy độ dài cạnh của lục giác đều cần tìm là 25/√3


g, 18 - (\(x\) + 14) : 3 = 27
(\(x\) + 14) : 3 = 18 - 27
(\(x\) + 14) : 3 = - 9
\(x\) + 14 = - 9 x 3
\(x\) + 14 = -27
\(x\) = - 27 - 14
\(x\) = - 41
h, 132 - 2.(\(x\) - 4) = 46
2.(\(x\) - 4) = 132 - 46
2.(\(x\) - 4) = 86
\(x\) - 4 = 86 : 2
\(x\) - 4 = 43
\(x\) = 43 + 4
\(x\) = 47

(-24). 72 - 72 . 26 - 50 .28
= 72. [(-24) - 26] - 50. 28
= 72. (-50) - 50. 28
= 72. (-50) + (-50). 28
= (-50). ( 72 + 28 )
= (-50). 100
= -5000

a, \(xy\) = \(x\) - y
\(xy\) + y = \(x\)
y.(\(x\) + 1) = \(x\)
y = \(\dfrac{x}{x+1}\) (đk \(x\) ≠ -1)
y nguyên ⇔ \(x\) ⋮ \(x\) + 1
⇒ \(x\) + 1 - 1 ⋮ \(x\) + 1
1 ⋮ \(x\) + 1
\(x\) + 1 \(\in\) Ư(1) = {-1; 1}
lập bảng ta có:
| \(x+1\) | -1 | 1 |
| \(x\) | -2 | 0 |
| y = \(\dfrac{x}{x+1}\) | 2 | 0 |
| (\(x\);y) | (-2;2) | (0;0) |
Theo bảng trên ta có các cặp \(x\); y nguyên thỏa mãn đề bài là:
(\(x\); y) = (-2; 2); (0; 0)

Lời giải:
$-(-17+156)+(483-144)-(-18)=17-156+483-144+18$
$=483-(156+144)+(17+18)$
$=483-300+35=183+35=218$

-3 \(\in\) Z. Vì Z là tập hợp số nguyên gồm số nguyên âm, số 0 và số nguyên dương.
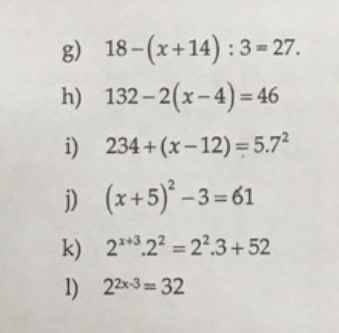
Vì đóng vào các hộp mỗi hộp 10 chiếc,24 chiếc hoặc 45 chiếc thì vừa đủ nên số khẩu tranhg là bội của 10; 24; 45
Gọi số khẩu trang là \(x\) (khẩu trang) 1 000 ≤ \(x\) ≤ 1 200; \(x\) \(\in\) N
Theo bài ra ta có: \(x\) \(\in\) BC(10; 24; 45)
10 = 2.5; 24 = 23.8; 45 = 32.5; BCNN(10; 24; 45) = 23.32.5 = 360
\(x\) \(\in\) BC(10;24;45) = {0; 360; 720; 1080;1440;..;}
Vì 1000 ≤ \(x\) ≤ 1200 nên \(x\) = 1080
Vậy công ty đó sản xuất được 1080 cái khẩu trang.