Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


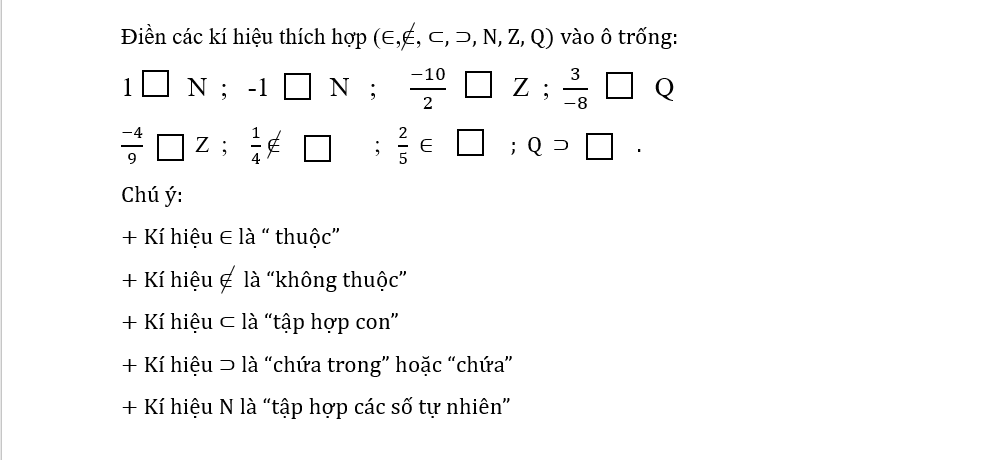
\(-3\notin N\)
\(\dfrac{-1}{2}\in Q\)
\(\dfrac{7}{9}\in Q\)
\(N\subset Z\subset Q\)

a: \(11\in N;11\in Q;11\in Z\)
b: \(-26\in Q;-26\in Z\)
c: \(\dfrac{1}{5}\in Q\)
d: \(-\dfrac{3}{4}\in Q\)

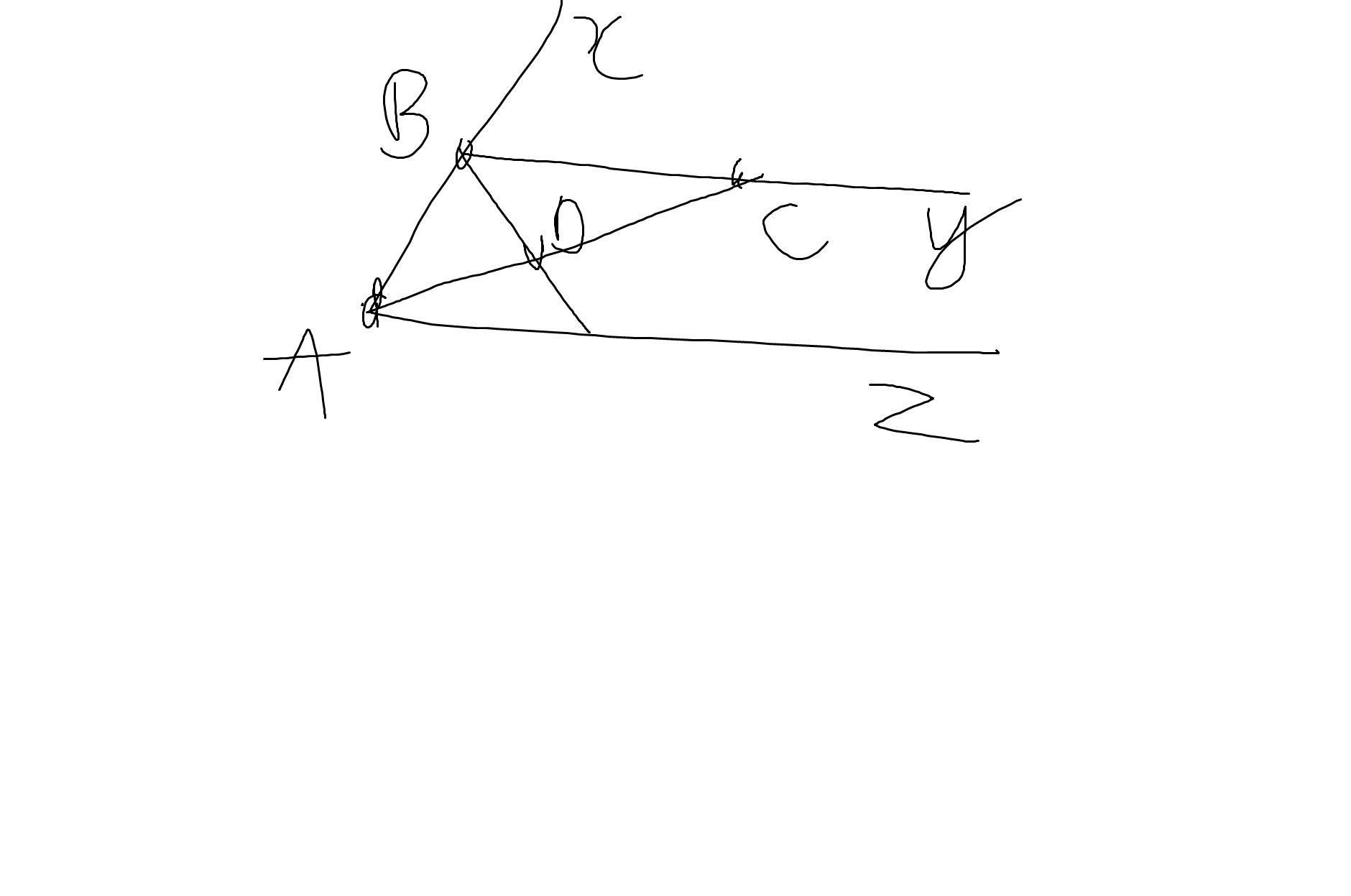
Ta có: QE\(\perp\)OM
NP\(\perp\)OM
Do đó: QE//NP
Ta có: PQ\(\perp\)Ox
MN\(\perp\)Ox
Do đó: PQ//MN

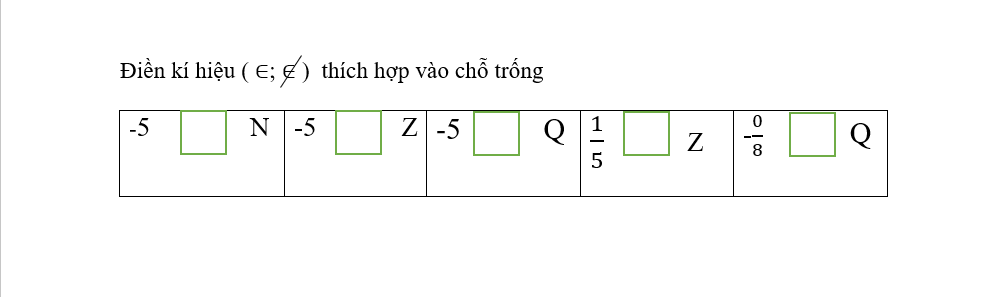
\(-5\notin N\\ -5\in Z\\- 5\in Q\\ \dfrac{1}{5}\notin Z\\ -\dfrac{0}{8}\in Q\)

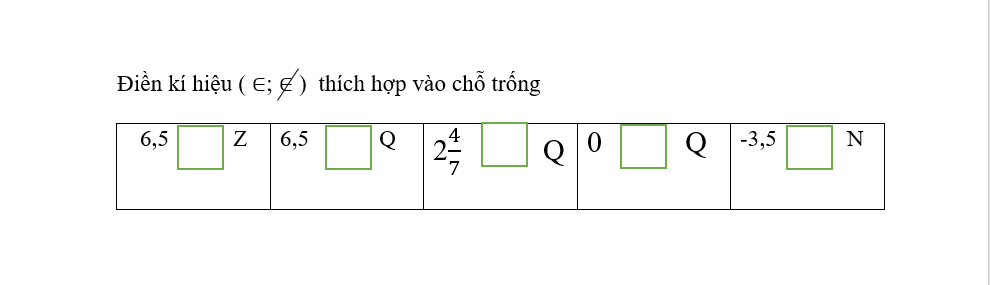
\(6,5\notin Z\\ 6,5\in Q\\ 2\dfrac{4}{7}\notin Q\\ 0\in Q\\ -3,5\notin N\)

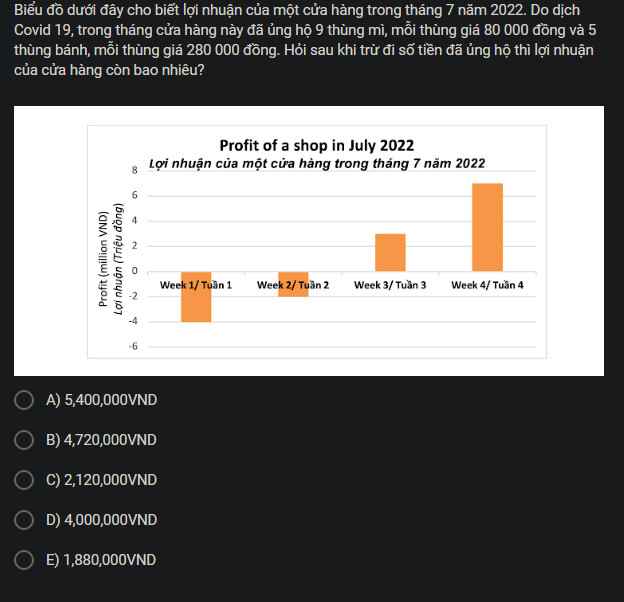
Số tiền lợi nhuận ban đầu là:
-4-2+3+7=10-6=4(triệu đồng)
Số tiền đã chi ra là:
\(9\cdot80000+5\cdot280000=2120000\left(đồng\right)=2,12\left(triệuđồng\right)\)
Số tiền còn lại là:
4-2,12=1,88(triệu đồng)
=>Chọn E

a: Ta có: \(\widehat{xBy}=\widehat{xAz}\left(=60^0\right)\)
mà hai góc này là hai góc ở vị trí đồng vị
nên By//Az
b: Ta có: \(\widehat{ABC}+\widehat{xBC}=180^0\)(hai góc kề bù)
=>\(\widehat{ABC}+60^0=180^0\)
=>\(\widehat{ABC}=120^0\)
AC là phân giác của góc zAB
=>\(\widehat{BAC}=\dfrac{\widehat{xAB}}{2}=30^0\)
Xét ΔBAC có \(\widehat{ABC}+\widehat{BAC}+\widehat{BCA}=180^0\)
=>\(\widehat{BCA}+120^0+30^0=180^0\)
=>\(\widehat{BCA}=30^0\)
c: Ta có: BD là phân giác của góc ABC
=>\(\widehat{ABD}=\dfrac{\widehat{ABC}}{2}=60^0\)
Xét ΔDBA có \(\widehat{DBA}+\widehat{DAB}=60^0+30^0=90^0\)
nên ΔBDA vuông tại D
=>BD\(\perp\)AC

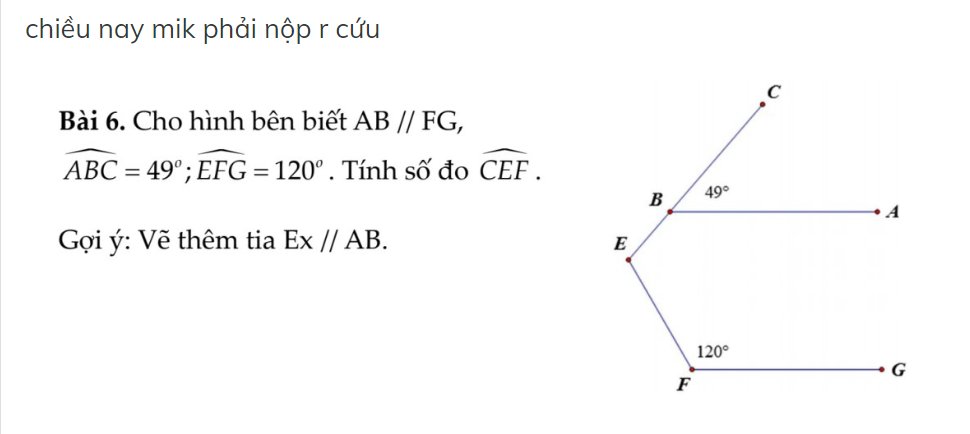
Kẻ Ex // AB
\(\widehat{BEx}\) = \(\widehat{CBA}\) = 490 (đồng vị)
\(\widehat{xEF}\) + \(\widehat{EFG}\) = 1800 (hai góc trong cùng phía)
⇒ \(\widehat{xEF}\) = 1800 - \(\widehat{EFG}\) = 1800 - 1200 = 600
\(\widehat{BEF}\) = \(\widehat{BEx}\) + \(\widehat{xEF}\) = 490 + 600 = 1090
Kết luận: góc BEF là 1090
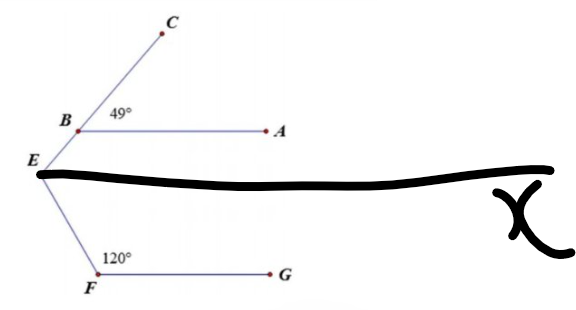
Kẻ Ex//AB(Ex và AB nằm trên cùng mặt phẳng bờ chứa tia BE)
Ta có: Ex//AB
AB//FG
Do đó: Ex//FG
Ex//AB
=>\(\widehat{BEx}=\widehat{CBA}\)(hai góc đồng vị)
=>\(\widehat{xEB}=49^0\)
Ta có: Ex//FG
=>\(\widehat{xEF}+\widehat{EFG}=180^0\)
=>\(\widehat{xEF}=180^0-120^0=60^0\)
\(\widehat{BEF}=\widehat{xEB}+\widehat{xEF}=49^0+60^0=109^0\)



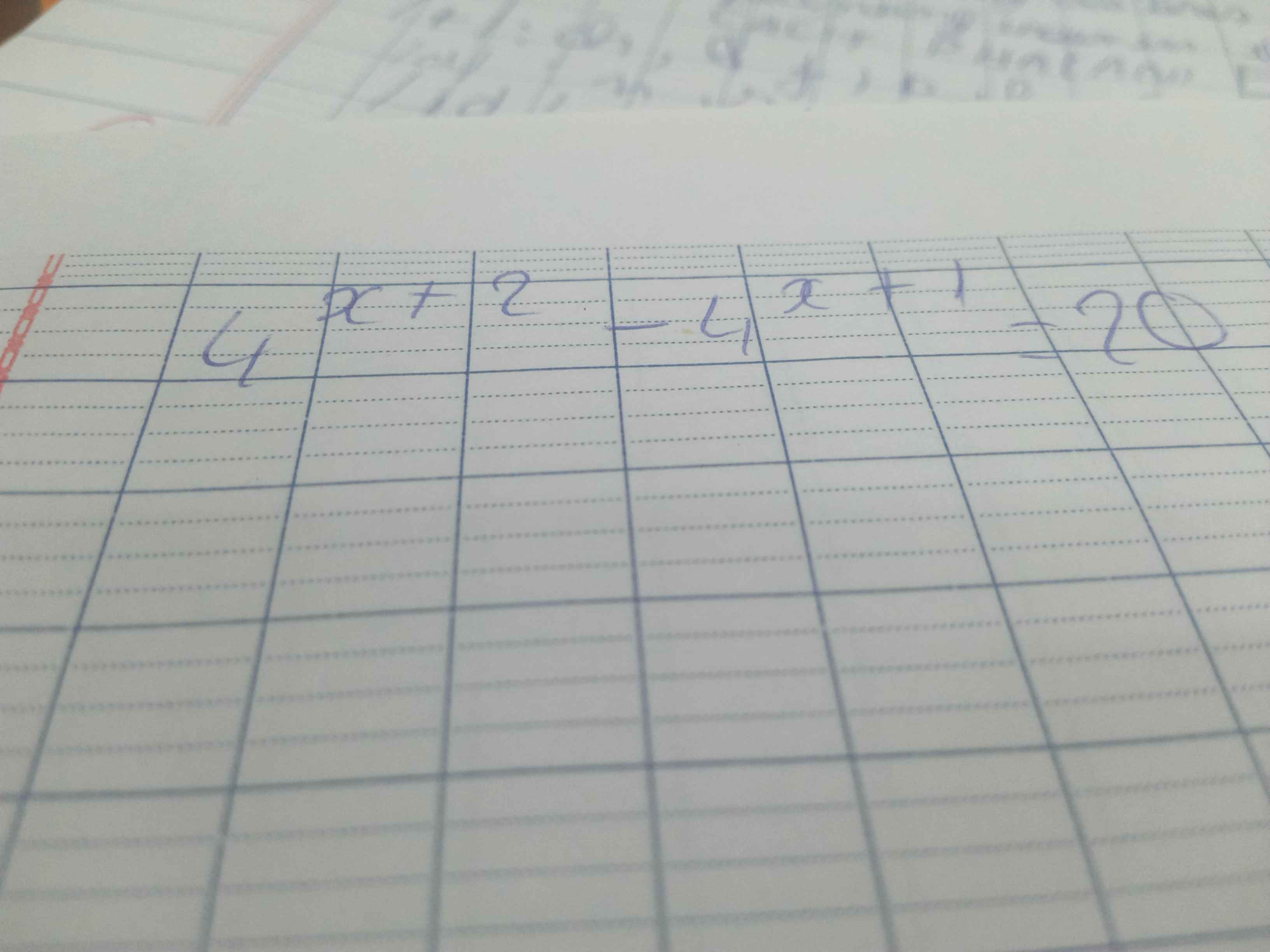

\(1\in\mathbb{N}\\ -1\notin\mathbb{N}\\ \dfrac{-10}{2}\in\mathbb{Z}\\\dfrac{3}{-8}\in\mathbb{Q}\\ \dfrac{-4}{9}\notin\mathbb{Z}\\\dfrac{1}{4}\notin\mathbb{N};\left(\mathbb{Z}\right) \\\dfrac{2}{5}\in\mathbb{Q}\\\mathbb{Q}\supset\mathbb{N};\left(\mathbb{Z}\right)\)