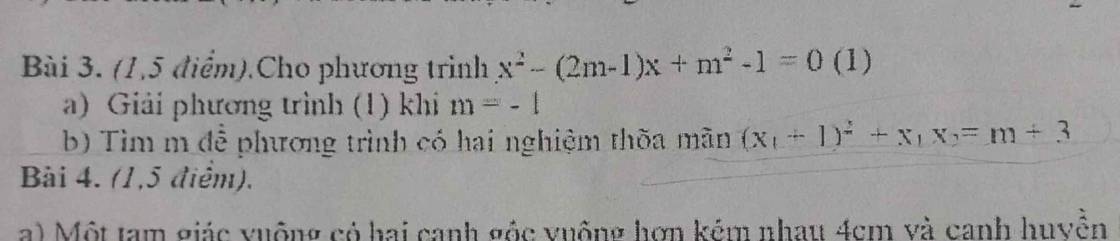 giải giúp mình câu b ạ
giải giúp mình câu b ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


16\(\dfrac{10}{13}\) + 3\(\dfrac{3}{13}\) - 8 x 12,5%
= 16 + \(\dfrac{10}{13}\) + 3 + \(\dfrac{3}{13}\) - 1
= (16 + 3) + (\(\dfrac{10}{13}+\dfrac{3}{13}\)) - 1
= 19 + 1 - 1
= 19 + (1 - 1)
= 19
\(16\dfrac{10}{13}+3\dfrac{3}{13}-8x12,5\%\)
=\(20-8x12.5\%\)
=\(20-1=19\)

\(x:0,1-x:0,25\) + \(x:50\%\) = 84,8 + 56
\(x\) x 10 - \(x\) x 4 + \(x\) x 2 = 140,8
\(x\) x (10 - 4 + 2) = 140,8
\(x\) x 8 = 140,8
\(x\) = 140,8 : 8
\(x=17,6\)
x:0,1-x:0,25+x:50%=84,8+56
Xx10-Xx4+Xx2=140,8
Xx(10-4+2)=140,8
Xx8=140.8
X=140.8:8
x=17,6

Bạn nên viết lại đề cho rõ ràng để mọi người đọc hiểu và hỗ trợ nhanh hơn nhé.

\(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{43\cdot45}\\ =\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{43}-\dfrac{1}{45}\\ =\dfrac{1}{1}-\dfrac{1}{45}\\ =\dfrac{44}{45}\)
A = \(\dfrac{2}{1.3}\) + \(\dfrac{2}{3.5}\) + ... + \(\dfrac{2}{43.45}\)
A = \(\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{43}-\dfrac{1}{45}\)
A = \(\dfrac{1}{1}-\dfrac{1}{45}\)
A = \(\dfrac{44}{45}\)

Giải:
Hiệu số tuổi của hai mẹ con luôn không đổi theo thời gian, 3 năm nữa mẹ vẫn hơn con 28 tuồi.
Ta có sơ đồ:
Theo sơ đồ ta có:
Tuổi mẹ 3 năm nữa là: 28 :(7 - 3) x 7 = 49 (tuổi)
Tuổi mẹ hiện nay là: 49 - 3 = 46 (tuổi)
Tuổi con hiện nay là: 46 - 28 = 18 (tuổi)
Đáp số: Tuổi con hiện nay là 18 tuổi
Tuổi mẹ hiện nay là 46 tuồi

Lời giải:
\(P=\frac{x+7\sqrt{x}}{x+2\sqrt{x}}=\frac{x+2\sqrt{x}+5\sqrt{x}}{x+2\sqrt{x}}=1+\frac{5\sqrt{x}}{x+2\sqrt{x}}=1+\frac{5}{\sqrt{x}+2}\)
Với $x$ là số nguyên không âm, để $P$ nguyên thì $\sqrt{x}+2$ là ước của 5.
Mà $\sqrt{x}+2\geq 2$ với mọi $x$ nguyên không âm
$\Rightarrow \sqrt{x}+2=5$
$\Rightarrow \sqrt{x}=3$
$\Rightarrow x=9$ (tm)



Bạn xem lại đề. Kết quả ra $m$ khá xấu, không phù hợp với bài toán PT bậc 2 cơ bản.