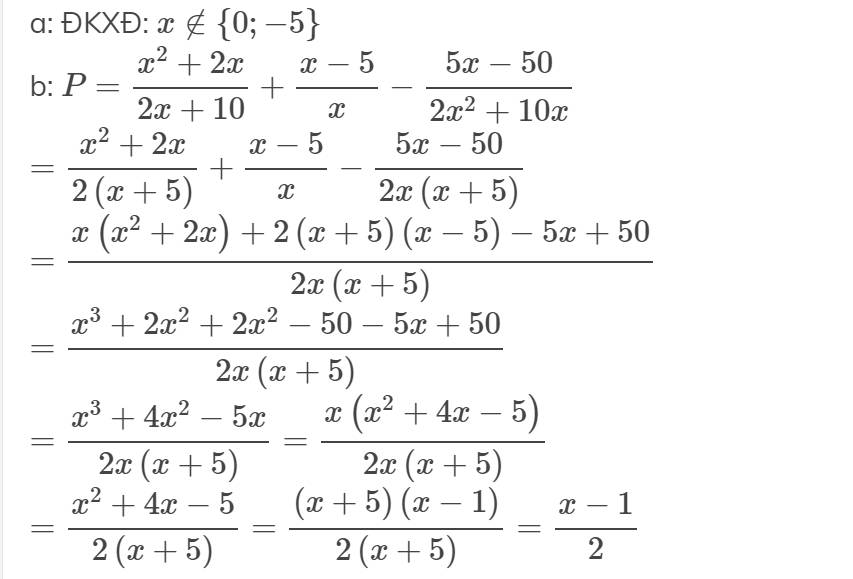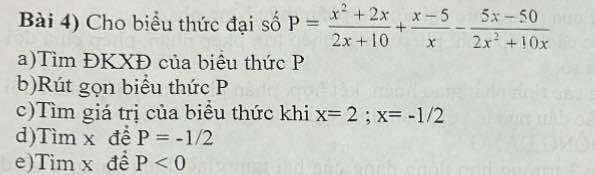có sai hay chữ xấu thì mong bạn thông cảm nhaaaa

  nếu sai hay chữ xấu mong bạn thông cảm nhaaaa

bài 9:

a: Xét ΔAHB vuông tại H và ΔBCD vuông tại C có

\(\widehat{ABH}=\widehat{BDC}\)(hai góc so le trong, AB//CD)

Do đó: ΔAHB~ΔBCD

b: ta có: ΔABD vuông tại A

=>\(AB^2+AD^2=BD^2\)

=>\(BD^2=9^2+12^2=225=15^2\)

=>BD=15(cm)

Ta có: ΔAHB~ΔBCD

=>\(\dfrac{AH}{BC}=\dfrac{AB}{BD}\)

=>\(\dfrac{AH}{9}=\dfrac{12}{15}\)

=>\(AH=9\cdot\dfrac{12}{15}=9\cdot\dfrac{4}{5}=7,2\left(cm\right)\)

Bài 10:

a: Xét ΔOEA vuông tại E và ΔODB vuông tại D có

\(\widehat{EOA}=\widehat{DOB}\)(hai góc đối đỉnh)

Do đó: ΔOEA~ΔODB

=>\(\dfrac{OE}{OD}=\dfrac{OA}{OB}\)

=>\(OE\cdot OB=OA\cdot OD\)

b: Xét ΔCEB vuông tại E và ΔCDA vuông tại D có

\(\widehat{ECB}\) chung

Do đó: ΔCEB~ΔCDA

=>\(\dfrac{CE}{CD}=\dfrac{CB}{CA}\)

=>\(\dfrac{CE}{CB}=\dfrac{CD}{CA}\)

Xét ΔCED và ΔCBA có

\(\dfrac{CE}{CB}=\dfrac{CD}{CA}\)

\(\widehat{ECD}\) chung

Do đó: ΔCED~ΔCBA

Bài 7:

a: Xét ΔOBA và ΔOCD có

\(\widehat{OBA}=\widehat{OCD}\)

\(\widehat{BOA}=\widehat{COD}\)(hai góc đối đỉnh)

Do đó: ΔOBA~ΔOCD

b: Ta có: ΔOBA~ΔOCD

=>\(\dfrac{OB}{OC}=\dfrac{OA}{OD}\)

=>\(\dfrac{OB}{OA}=\dfrac{OC}{OD}\)

Xét ΔOBC và ΔOAD có

\(\dfrac{OB}{OA}=\dfrac{OC}{OD}\)

\(\widehat{BOC}=\widehat{AOD}\)(hai góc đối đỉnh)

Do đó: ΔOBC~ΔOAD

c: Ta có: ΔOBC~ΔOAD

=>\(\widehat{OCB}=\widehat{ODA}\)

Xét ΔEBD và ΔEAC có

\(\widehat{EDB}=\widehat{ECA}\)

\(\widehat{E}\) chung

Do đó: ΔEBD~ΔEAC

=>\(\dfrac{EB}{EA}=\dfrac{ED}{EC}\)

=>\(EB\cdot EC=EA\cdot ED\)

Bài 8:

Xét ΔHEA vuông tại E và ΔHDB vuông tại D có

\(\widehat{EHA}=\widehat{DHB}\)(hai góc đối đỉnh)

Do đó: ΔHEA~ΔHDB

=>\(\dfrac{HE}{HD}=\dfrac{HA}{HB}\)

=>\(HE\cdot HB=HD\cdot HA\)(1)

Xét ΔHFB vuông tại F và ΔHEC vuông tại E có

\(\widehat{FHB}=\widehat{EHC}\)(hai góc đối đỉnh)

Do đó: ΔHFB~ΔHEC

=>\(\dfrac{HF}{HE}=\dfrac{HB}{HC}\)

=>\(HF\cdot HC=HB\cdot HE\left(2\right)\)

Từ (1) và (2) suy ra \(HA\cdot HD=HF\cdot HC=HB\cdot HE\)

Khi giải toán hình Thịnh cần có thêm hình vẽ nhé.

Bài 5:

a: Xét ΔABC vuông tại A và ΔHAC vuông tại H có

\(\widehat{ACB}\) chung

Do đó: ΔABC~ΔHAC

b: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có

\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{HAC}\right)\)

Do đó: ΔHAB~ΔHCA

=>\(\dfrac{HA}{HC}=\dfrac{HB}{HA}\)

=>\(HA^2=HB\cdot HC\)

c: Ta có: ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(AC^2=10^2-6^2=64\)

=>AC=8(cm)

Bài 6:

a: Xét ΔABO và ΔDCO có

\(\widehat{AOB}=\widehat{DOC}\)(hai góc đối đỉnh)

\(\widehat{OAB}=\widehat{ODC}\)

Do đó; ΔABO~ΔDCO

b: Ta có: ΔOAB~ΔODC

=>\(\dfrac{OA}{OD}=\dfrac{OB}{OC}\)

=>\(\dfrac{OA}{OB}=\dfrac{OD}{OC}\)

Xét ΔOAD và ΔOBC có

\(\dfrac{OA}{OB}=\dfrac{OD}{OC}\)

\(\widehat{AOD}=\widehat{BOC}\)(hai góc đối đỉnh)

Do đó: ΔOAD~ΔOBC

a: ĐKXĐ: \(x\notin\left\{0;-5\right\}\)

b: \(P=\dfrac{x^2+2x}{2x+10}+\dfrac{x-5}{x}-\dfrac{5x-50}{2x^2+10x}\)

\(=\dfrac{x^2+2x}{2\left(x+5\right)}+\dfrac{x-5}{x}-\dfrac{5x-50}{2x\left(x+5\right)}\)

\(=\dfrac{x\left(x^2+2x\right)+2\left(x+5\right)\left(x-5\right)-5x+50}{2x\left(x+5\right)}\)

\(=\dfrac{x^3+2x^2+2x^2-50-5x+50}{2x\left(x+5\right)}\)

\(=\dfrac{x^3+4x^2-5x}{2x\left(x+5\right)}=\dfrac{x\left(x^2+4x-5\right)}{2x\left(x+5\right)}\)

\(=\dfrac{x^2+4x-5}{2\left(x+5\right)}=\dfrac{\left(x+5\right)\left(x-1\right)}{2\left(x+5\right)}=\dfrac{x-1}{2}\)

c: Thay x=2 vào P, ta được:

\(P=\dfrac{2-1}{2}=\dfrac{1}{2}\)

Thay x=-1/2 vào P, ta được:

\(P=\dfrac{-\dfrac{1}{2}-1}{2}=-\dfrac{3}{2}:2=-\dfrac{3}{4}\)

d: P=-1/2

=>\(\dfrac{x-1}{2}=\dfrac{-1}{2}\)

=>x-1=-1

=>x=0(loại)

e: Để P<0 thì \(\dfrac{x-1}{2}< 0\)

=>x-1<0

=>x<1

Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}x< 1\\x\notin\left\{0;-5\right\}\end{matrix}\right.\)

Bàu 2

\(n_P=\dfrac{1,55}{31}=0,05mol\\ a)4P+5O_2\xrightarrow[]{t^0}2P_2O_5\)

0,05        0,0625       0,025

\(b)m_{P_2O_5}=0,025.142=3,55g\\ c)V_{O_2}=0,0625.24,79=1,549375l\)

Bài 3

\(a)n_{Fe}=\dfrac{11,2}{56}=0,2mol\\ Fe+2HCl\rightarrow FeCl_2+H_2\)

0,2      0,4             0,2           0,2

\(V=V_{H_2}=0,2.24,79=4,958l\\ b)m_{FeCl_2}=0,2.127=25,4g\\ c)m_{ddHCl}=\dfrac{0,4.36,5}{20\%}\cdot100\%=73g\\ d)m_{dd}=11,2+73-0,2.2=83,8g\\ C_{\%FeCl_2}=\dfrac{25,4}{83,8}\cdot100\%=30,31\%\)

Bước 1: Lấy một ít dung dịch từ mỗi lọ vào 3 ống nghiệm riêng biệt.

Bước 2: Nhúng quỳ tím vào từng ống nghiệm:

- Quỳ tím chuyển sang màu đỏ: Dung dịch HCl có tính axit.
- Quỳ tím chuyển sang màu xanh: Dung dịch NaOH có tính bazơ.
- Quỳ tím không đổi màu: Dung dịch MgCl₂ trung tính.
Bước 3: Nhỏ vài giọt phenolphtalein vào ống nghiệm chứa dung dịch NaOH. Dung dịch chuyển sang màu hồng.

Kết luận:

- Dung dịch HCl: Quỳ tím chuyển sang màu đỏ.
- Dung dịch NaOH: Quỳ tím chuyển sang màu xanh, và chuyển sang màu hồng khi thêm phenolphtalein.
- Dung dịch MgCl₂: Quỳ tím không đổi màu.

- Các thành phần chính của mô đun cảm biến nhiệt độ, độ ẩm, ánh sáng gồm:

+ Cảm biến.

+ Bộ xử lý tín hiệu.

+ Giao tiếp.

- Nguyên lý hoạt động:

+ Cảm biến nhiệt độ là dựa trên sự thay đổi điện trở của vật liệu dẫn điện khi nhiệt độ thay đổi.

+ Cảm biến độ ẩm sử dụng nguyên lý đo điện trở của vật liệu hấp thụ nước để xác định độ ẩm của môi trường.

+ Cảm biến ánh sáng sử dụng nguyên lý đo sự phản xạ hoặc hấp thụ của ánh sáng để xác định mức độ chiếu sáng.