Lời giải:
Trong 1 giờ người thứ nhất làm được:

$1:6=\frac{1}{6}$ (công việc) 

Nếu 3 người làm chung thì sau 1 giờ làm được:

$\frac{3}{10}+\frac{1}{6}=\frac{7}{15}$ (công việc)

Số phần công việc chưa hoàn thành là:

$1-\frac{7}{15}=\frac{8}{15}$

Lời giải:

Số thứ nhất = $\frac{4}{3}$ số thứ hai

Số thứ nhất = $\frac{10}{9}$ (số thứ hai + 60)

Vậy $\frac{4}{3}$ số thứ hai bằng $\frac{10}{9}$ (số thứ hai + 60)

Tỉ số số thứ hai lúc trước và sau là:

$\frac{10}{9}: \frac{4}{3}=\frac{5}{6}$

Hiệu số số thứ hai lúc sau và trước: $60$

Số thứ hai là: $60:(6-5)\times 5=300$ 

Số thứ nhất là: $300\times \frac{4}{3}=400$ 

Lời giải:
$(1-\frac{1}{2})(1-\frac{1}{3})(1-\frac{1}{4})...(1-\frac{1}{2011})$

$=\frac{1}{2}.\frac{2}{3}.\frac{3}{4}....\frac{2010}{2011}$
$=\frac{1.2.3...2010}{2.3.4...2011}$
$=\frac{1}{2011}$

Lời giải:
Không mất tính tổng quát giả sử $a\geq b\geq c$.

$\Rightarrow \frac{1}{a}\leq \frac{1}{b}\leq \frac{1}{c}$

Khi đó:
$\frac{4}{5}=\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\leq \frac{3}{c}$

$\Rightarrow 4c\leq 15<16\Rightarrow c<4$
Mà $c$ nguyên dương nên $c=1,2,3$

Nếu $c=1$ thì:

$\frac{1}{a}+\frac{1}{b}=\frac{4}{5}-\frac{1}{c}=\frac{4}{5}-1=\frac{-1}{5}<0$ (vô lý do $a>0, b>0$)

Nếu $c=2$ thì:

$\frac{1}{a}+\frac{1}{b}=\frac{4}{5}-\frac{1}{2}=\frac{3}{10}$

Do $\frac{1}{a}\leq \frac{1}{b}$ nên:

$\frac{3}{10}=\frac{1}{a}+\frac{1}{b}\leq \frac{2}{b}$

$\Rightarrow 3b< 20< 21\Rightarrow b< 7$

Thử các TH: $b=2,3,4,5,6$ thấy với $b=4$ thì $a=20$; $b=5$ thì $a=10$

Nếu $c=3$ thì:

$\frac{1}{a}+\frac{1}{b}=\frac{4}{5}-\frac{1}{3}=\frac{7}{15}\leq \frac{2}{b}$

$\Rightarrow 7b\leq 30< 35$

$\Rightarrow b< 5$. Mà $b\geq c=3$ nên $b=3$ hoặc $b=4$

Thử 2 TH trên thấy đều không thỏa mãn.

Vậy $(a,b,c)=(10,5,2), (20, 4,2)$ và hoán vị 

Ta có:

n + 2 = n + 1 + 1

Để (n + 2)/(n + 1) là số nguyên thì 1 ⋮ (n + 1)

n + 1 ∈ Ư(1) = {-1; 1}

n + 1 ∈ {-2; 0}

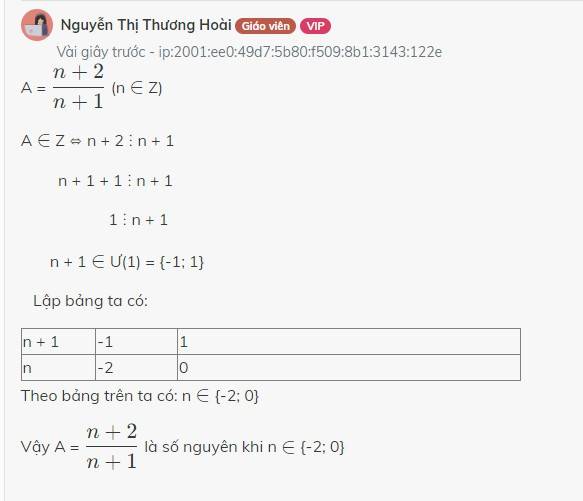
A = \(\dfrac{n+2}{n+1}\) (n \(\in\) Z)

A \(\in\) Z ⇔ n + 2 ⋮ n + 1 

         n + 1 + 1 ⋮ n + 1

                     1 ⋮ n + 1

       n + 1 \(\in\) Ư(1) = {-1; 1}

   Lập bảng ta có: 

Theo bảng trên ta có: n \(\in\) {-2; 0}

Vậy A = \(\dfrac{n+2}{n+1}\) là số nguyên khi n \(\in\) {-2; 0}

có thể tính là n+2/n+1 = n/n + 2/1 ko

Lời giải:
Với $n$ nguyên, để $\frac{n+2}{n+1}$ là số nguyên thì:

$n+2\vdots n+1$

$\Rightarrow (n+1)+1\vdots n+1$

$\Rightarrow 1\vdots n+1$

$\Rightarrow n+1\in\left\{1; -1\right\}$

$\Rightarrow n\in\left\{0; -2\right\}$

ĐKXĐ: n<>-1

Để \(\dfrac{n+2}{n+1}\) là số nguyên thì \(n+2⋮n+1\)

=>\(n+1+1⋮n+1\)

=>\(1⋮n+1\)

=>\(n+1\in\left\{1;-1\right\}\)

=>\(n\in\left\{0;-2\right\}\)