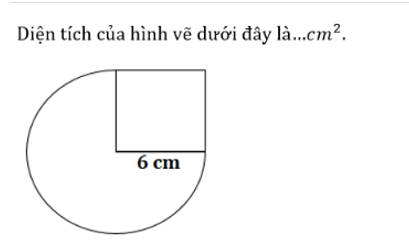
(1,5 điểm)
1. Nguồn điện là gì? Hãy kể tên 5 loại nguồn điện mà em biết.
2. Điện thoại di động sử dụng nguồn điện là pin sạc.
a) Khi ta không sử dụng, tắt nguồn điện thoại và cắm vào ổ điện để sạc pin thì pin trong điện thoại là nguồn điện hay dụng cụ tiêu thụ điện?
b) Nếu pin không phải là nguồn điện thì lúc này nguồn điện ở đâu?
3. Để thắp sáng hay tắt một bóng đèn thì cần có những thiết bị điện nào? Phải làm gì với những thiết bị đó? Em hãy minh họa bằng một mạch điện đơn giản.